Table of contents
Open Table of contents
- Visualización
- Análisis Exploratorio de Datos (Estadística Descriptiva)
- Correlación:
- Inferencia
- Regresión
- A manera de cierre
- Bibliografía
Visualización
Los siguientes temas podrían incluirse en Análisis exploratorio, si no se han incluid ya explícitamente en Visualización
- Scatterplots. PSDS, pg.34
- Histogramas. DSPP, pg. 89
Análisis Exploratorio de Datos (Estadística Descriptiva)
Introducción
Con la creciente digitalización de muchas actividades humanas cada vez es más sencillo acceder a variadas fuentes de datos. Idealmente antes de recopilar los datos hay un proceso de diseño experimental, en el que se definen unos objetivos y se plantean unas hipótesis; aunque no siempre es el caso.
Una vez tenemos los datos es importante describirlos o caracterizarlos. Aquí entra el Análisis Exploratorio de datos. Éste método es una revisión de la estructura de los datos, y su fortaleza está en usar gráficos y visualizaciones para ese proceso de obtener información que pueda usarse en formular o refutar validar las hipótesis relativas a las variables bajo estudio; como también validar las suposiciones que tengamos sobre ellas.
Aquí seguimos el libro de Chen1, que propone las siguientes fases.
| Fase | Preguntas comunes |
|---|---|
| Coherencia conceptual de los datos | ¿Cómo se recogieron los datos? |
| ¿Que fuentes potenciales de error hay en los datos? | |
| ¿Qué significa cada variable? | |
| ¿Que unidades de medida tiene la variable y tiene sentido para el análisis que se plantea hacer? | |
| Preprocesamiento | ¿Estamos leyendo/interpretando los tipos de datos de manera adecuada? |
| ¿Que manipulaciones son necesarias para asignar/definir las variables en la forma requerida (por ejemplo, como vector, como matriz, como conjunto de datos) | |
| ¿Es necesario agregar los datos? | |
| Calidad de la Señal | ¿es posible determinar la tendencia central? |
| ¿A que típo de distribución se asemeja más? | |
| ¿Hay una dependencia temporal o espacial en los datos? | |
| Identificación de datos problemáticos | ¿las gráficas muestran datos posiblemente errados? |
| ¿Al graficar como serie, hay datos que tengan valores muy diferentes a los demás? | |
| ¿Hay datos faltantes? | |
| Identificación de variables importantes | ¿Hay variables correlacionadas? |
| ¿Se puede hacer una modificación para mejorar la correlación? |
Tipos de datos faltantes
Según Chen et al., existen tres tipos de datos faltantes:
-
Datos faltantes distribuidos completamente al azar. Los datos faltantes de una variable no están relacionados con las demás variables del conjunto de datos. Usualmente esto no afecta el análisis.
-
Datos faltantes distribuidos al azar. Los datos faltantes dependen de otra variable. Por ejemplo, quienes no responden una pregunta de ingreso tienden a tener un bajo nivel educativo. Aquí normalmente es a lugar hacer un ajuste.
-
Datos faltantes no distribuidos al azar. Los datos faltantes se correlacionan con un concepto medido. Por ejemplo, las personas pueden no responder a la pregunta sobre el ingreso porque tienen altos ingresos. En estos casos se requiere conocer profundamente la teoría relacionada con la encuesta para poder analizar.
Además proponemos la siguiente categoría:
- Datos faltantes no necesarios. Cuando no se registra el valor porque la definición de la variable o de otra variable implica que el dato mismo no tiene sentido. Por ejemplo, a un bebé no se le pregunta si ha tenido hijos.
Coeficiente de Sesgo
En una distribución simétrica habrá en términos generales el mismo número de valores por encima o por debajo del promedio. Cuando hay un desbalance entre los valores arriba y abajo del promedio se habla de un sesgo.
-
Los datos de una distribución tienen un sesgo positivo cuando existen unos pocos valores que están muy alejados por encima del promedio (y la distribución no hay valores muy alejados por debajo del promedio)
-
Los datos de una distribución tienen un sesgo negativo cuando existen unos pocos valores que están muy alejados por debamo del promedio (y la distribución no hay valores muy alejados por encima del promedio)
Matemáticamente el valor de sesgo se calcula mediante:
Como la expresión está elevada al cubo, los valores negativos ( menores que al elevarse al cubo mantienen su signo y si la diferencia es grande estamos sumando un valor negativo muy grande a la suma. De la misma forma si es mucho más grande que , la resta da un valor positivo, que al elevarse al cubo suma un valor muy grande a la suma.
Ejemplo: Amortización de la vivienda en Colombia.
El Departamento Nacional de Estadística de Colombia (Dane) publica los microdatos de diferentes proceso estadísticos que lleva a cabo. Tenemos por ejemplo la encuesta nacional de calidad de vida, que busca caracterizar dimensiones del bienestar, como la salud, educación, actividades laborales y tenencia de bienes del hogar2.
Enfoquémonos en la variable P5100, ¿Cuánto pagan mensualmente por cuota de amortización?. En la descripción del análisis
estadístico3 se explica la forma de recolección de datos de la
encuesta.
Revisemos la fase de coherencia conceptual:
| Fase | Preguntas comunes | Análisis |
|---|---|---|
| Coherencia conceptual de los datos | ¿Cómo se recogieron los datos? | Se describe en la sección ‘muestreo’ de la descripción de los datos3. |
| ¿Que fuentes potenciales de error hay en los datos? | En este caso puede haber datos faltantes, errores de unidades (ejemplo, registrar 1 en lugar de 1000000 para un millón), o errores al registrar con texto en lugar de valores numéricos. | |
| ¿Qué significa cada variable? | Se define como “el gasto en que incurre el hogar para cubrir el crédito de vivienda que ha adquirido”. | |
| ¿Que unidades de medida tiene la variable y tiene sentido para el análisis que se plantea hacer? | La descripción de la variable indica ”$”, es necesario confirmarlo mediante el análisis exploratorio. |
Descargamos los datos de la página del Dane, en este caso el archivo de Tenencia y financiación de la vivienda que ocupa, de la página del dane 4. Descomprimimos los datos desde el sistema operativo.
Comenzamos con el preprocesamiento. Inicialmente incluímos las librerías:
# coding: utf-8
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
Cerramos las ventanas que puedan estar abiertas:
plt.close('all')
plt.ion()
En Python procedemos a cargar los datos
datos = pd.read_csv('Tenencia y financiación de la vivienda que ocupa el hogar.CSV')
Nos hacemos la pregunta:
| Fase | Preguntas comunes | Análisis |
|---|---|---|
| Preprocesamiento | ¿Estamos leyendo/interpretando los tipos de datos de manera adecuada? | Para responder esta pregunta, imprimimos las variables. Como la información está guardada en el dataframe datos, esto se hace con la expresión: datos.columns. |
La salida de éste comando es el texto:
Index(['DIRECTORIO;SECUENCIA_ENCUESTA;SECUENCIA_P;ORDEN;FEX_C;P5095;P5100;P3197;P5120;P8692;P8692S1A1;P8692S2;P5610;P5610S1;P8693;P5110;P5130;P5140;P3006;P5650;P5160;P5160S1;P5160S1A1;P5160S2;P5160S2A1'], dtype='object')
Notese que se trata de una lista (se define porque abre el paréntesis
cuadrado [ y cierra con ]). Los elementos de las listas se separan
por comas, pero aquí tenemos punto y coma. Esto indica que
probablemente la primera línea, que debía tener varias variables, se
interpretó como una sóla variable.
Otra forma de verlo es imprimir la variable shape del DataFrame:
print(datos.shape)
Se obtiene (86405, 1), es decir, este DataFrame tiene 86405
registros, para una única variable. Otra forma de confirmar esta
situación errónea es usar la variable head del dataframe:
print(datos.head) 5:
bound method NDFrame.head of DIRECTORIO;SECUENCIA_ENCUESTA;SECUENCIA_P;ORDEN;FEX_C;P5095;P5100;P3197;P5120;P8692;P8692S1A1;P8692S2;P5610;P5610S1;P8693;P5110;P5130;P5140;P3006;P5650;P5160;P5160S1;P5160S1A1;P5160S2;P5160S2A1
0 7910114;1;1;1;282.37094522;3;;;;;;;;;;;;400000...
1 7910115;1;1;1;3.0542169534;6;;;;;;;;;;;200000;...
2 7910119;1;1;1;31.288476991;4;;;;;;;;;;;250000;...
3 7910120;1;1;1;73.57774897;1;;2;2;;;;0;;0;12000...
Vemos que los datos están separados por ;, entonces se deben indicar
que éste es el separador. Es decir:
datos = pd.read_csv('Tenencia y financiación de la vivienda que ocupa el hogar.CSV',sep=';')
Volvemos a revisar que se haya cargado bien, con datos.columns, obteniendo:
print(datos.columns)
Index(['DIRECTORIO', 'SECUENCIA_ENCUESTA', 'SECUENCIA_P', 'ORDEN', 'FEX_C',
'P5095', 'P5100', 'P3197', 'P5120', 'P8692', 'P8692S1A1', 'P8692S2',
'P5610', 'P5610S1', 'P8693', 'P5110', 'P5130', 'P5140', 'P3006',
'P5650', 'P5160', 'P5160S1', 'P5160S1A1', 'P5160S2', 'P5160S2A1'],
dtype='object')
Esto es una lista, separada por comas, donde hay 25 datos,
correspondientes a 25 variables. Esto también se ve de la variable
datos.shape, que ahora es la pareja: (86405, 25), es decir 86405
registros de 25 variables.
Explorando datos faltantes6
Los datos que nos interesan corresponden a la variable P5100,
entonces para estar seguros de que tenemos los datos de esa variable,
procedemos a imprimir los valores únicos. En Python se obtiene con:
datos.P5100.unique(). Aquí tenemos un vector de 271 elementos. El
primer número de ese vector es nan, o ‘Not A Number’, lo que
refuerza nuestra hipótesis de que en los datos podemos tener valores
faltantes.
Para construir un vector indique la posición de los valores faltantes,
usamos: datos.P5100.isnull(). La suma de éste vector nos dará el
número de datos faltantes: sum(datos.P5100.isnull()), en este caso
84745. La proporción de datos faltantes sería:
print(sum(datos.P5100.isnull())/len(datos.P5100))
Esto da una fracción de 0.98 del total de datos.
Revisando el diccionario de datos, existe otra variable relacionada.
| Pregunta | Código | Descripción | Opciones |
|---|---|---|---|
| ¿La vivienda ocupada por este hogar es? | P5095 | Con esta pregunta se quiere conocer la forma de tenencia de la vivienda que ocupa el hogar | 1. Propia, totalmente pagada 2. Propia, la están pagando 3. En arriendo o subarriendo 4. Con permiso del propietario, sin pago alguno (usufructuario) 5. Posesión sin título (ocupante de hecho) 6. Propiedad colectiva |
Entonces tenemos que los únicos registros donde debería haber un valor
de pago por amortización son quienes están pagando. O al contrario,
los que no deberían tener registro del valor son los que no están
pagando. Estos últimos registros no tienen un número 2 en la variable
P5095. Es decir, son los registros para los que: datos.P5095!=2. La
suma de estos valores se construye con: sum)datos.P5095!=2. Lo que
también nos dá como resultado 84745. Es decir, los valores faltantes
de la variable P5100 son faltantes no necesarios.
Continuamos el preprocesamiento:
| Fase | Preguntas comunes | Análisis |
|---|---|---|
| Preprocesamiento | ¿Que manipulaciones son necesarias para asignar/definir las variables en la forma requerida (por ejemplo, como vector, como matriz, como conjunto de datos) | Los datos están cargados en un DataFrame. Requerimos filtrar los datos faltantes. Para ello podemos definir una variable que corresponda a los valores no nulos. |
El comando es:
pagoamortizacion = datos.P5100[~datos.P5100.isnull()]
Estadísticos de centro
Continuamos con el preprocesamiento:
| Fase | Preguntas comunes | Análisis |
|---|---|---|
| Preprocesamiento | ¿Es necesario agregar los datos? | En este caso tiene sentido agregar, porque esperamos que la variable tenga una dispersión y justamente queremos saber cómo se distribuye. Para esto podemos calcular estadísticos de centro y variabilidad y construir un histograma. |
En Python los estadísticos de centro se hallan con la función describe:
print(pagoamortizacion.describe())
Y se obtiene:
count 1.660000e+03
mean 8.007266e+05
std 8.576620e+05
min 9.900000e+01
25% 3.000000e+05
50% 5.500000e+05
75% 1.000000e+06
max 9.000000e+06
Name: P5100, dtype: float64
Luego tenemos 1660 datos, con un promedio de 800726.6, un mínimo de 99 y un máximo de 9000000. Estos valores refuerzan la hipótesis de que la unidad de la variable son los pesos. Podemos planear entonces construir un histograma que tenga divisiones cada 500 mil pesos, desde 0 hasta 9 millones.
binamort = np.linspace(0,9e6,19)
Construimos el histograma normalizado:
plt.hist(pagoamortizacion,edgecolor='w',bins=binamort,density=True,label='histograma normalizado')
El análisis no está completo si no se incluyen las unidades de medida, y los nombres de las clases. Lo hacemos así:
binamortmillones = binamort/1e6 # para usar en el texto
xbinstxt = [str(binamortmillones[i])+' a '+str(binamortmillones[i+1]) for i in range(len(binamortmillones)-1)] # Genera el texto de las etiquetas
plt.subplots_adjust(bottom=0.2,left=0.2) # mejora el espacio abajo y la izquierda
plt.ticklabel_format(style = 'plain') # simplifica las unidades
plt.xlabel("Cuota (millones)") # texto en el eje x
plt.title("Pagos de amortización") # título de la gráfica
xbins = [(binamort[i]+binamort[i+1])/2 for i in range(len(binamort)-1)] # posición del texto de las clases
ax.set_xticks(xbins,xbinstxt,rotation=45) # texto de las clases
plt.legend()
Adicionalmente se puede incluir una aproximación continua a la
distribución. Una forma de hacerlo es usar la librería seaborn de
Python7. Chen et al. explican cómo hacerlo en R, en la página 91.
sns.kdeplot(data=pagoamortizacion,label="densidad",fill=True, alpha=0.6)
Adicionalmente se puede exportar la gráfica:
plt.savefig("amortizacion_ecv_23.png")
Con esto se obtiene la siguiente gráfica:
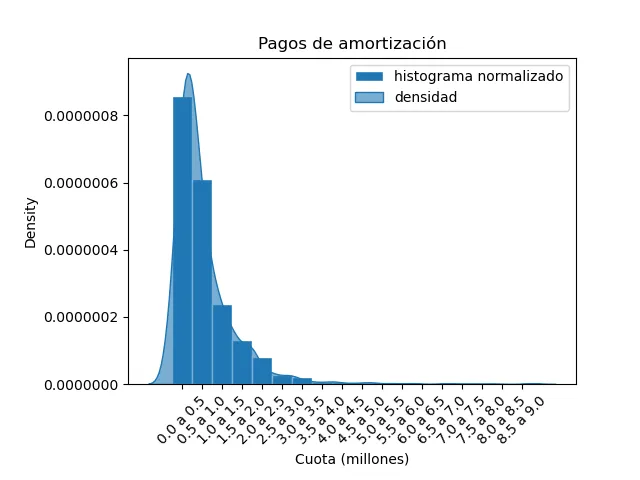
Continuamos con el análisis.
| Fase | Preguntas comunes | Análisis |
|---|---|---|
| Calidad de la Señal | ¿es posible determinar la tendencia central? | Calculamos el valor del promedio en alrededor de 800 mil pesos, y la mediana en 550 mil pesos como medidas de tendencia central |
| ¿A que típo de distribución se asemeja más? | Es una distribución unimodal, asimétrica, con cola a la izquierda. | |
| ¿Hay una dependencia temporal o espacial en los datos? | No tenemos información temporal en este conjunto de datos. La encuesta es en un momento del tiempo, luego la dependencia temporal podría revisarse comparando con otras versiones de la encuesta | |
| Identificación de datos problemáticos | ¿las gráficas muestran datos posiblemente errados? | No encontramos datos extraños. |
| ¿Hay datos faltantes? | Si, ya se discutió anteriormente. | |
| ¿Al graficar como serie, hay datos que tengan valores muy diferentes a los demás? | Construimos una gráfica de dispersión para los datos. En ésta gráfica no se ven valores atípicos. |
El diagrama de dispersión se genera con el siguiente código:
plt.figure()
plt.plot(pagoamortizacion,'.')
plt.title('valores amortización')
plt.xlabel('consecutivo')
plt.ticklabel_format(style = 'plain')
plt.savefig("amortizacion_consecutivo_ecv_23.png")
Obtenemos la siguiente gráfica:
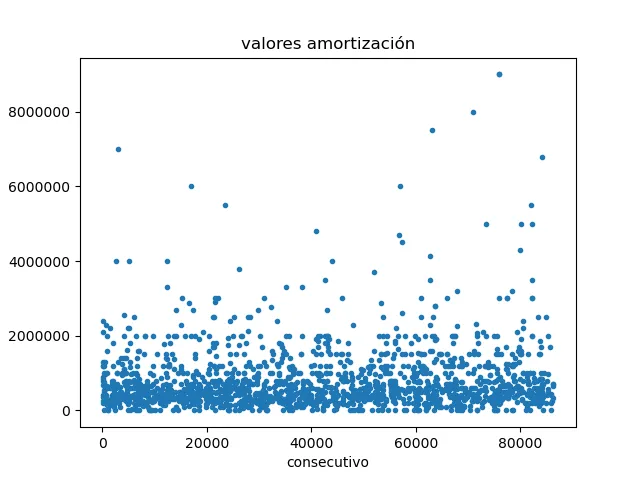
Aquí vemos que los puntos se distribuyen alrededor de el valor 500 mil, reforzando lo que habíamos encontrado anteriormente. No hay datos especialmente extraños.
Sesgo
El sesgo8 se calcula en Pandas usando la función skew del
DataFrame. En este caso tenemos:
print(pagoamortizacion.skew())
Obtenemos un valor de 3.705296, lo que corresponde a un sesgo positivo. Esto era de esperarse por la forma de la distribución que habíamos visto anteriormente.
Ejercicio, Edades en Cundinamarca
Utilizando los datos del Censo Nacional de Población y Vivienda 2018, lleve a cabo los análisis similares a los que hicimos en ésta sección para la variable de Edades. Encuentre los valores faltantes. El histograma debe ser similar al siguiente:
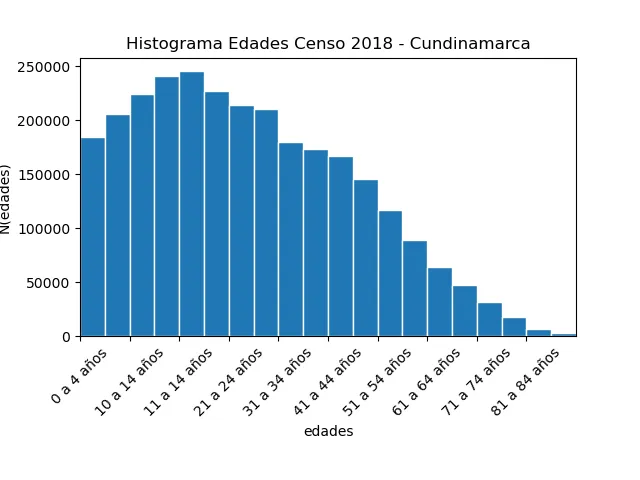
Construya también el diagrama de dispersión y analícelo.
Correlación9:
La correlación es una medida sobre que tanto están relacionadas dos variables. Toma valores numéricos en el intervalo . Por ejemplo, el coeficiente de correlación de Pearson se calcula multiplicando las desviaciones de la media de la primera variable con las desviaciones de la media de la segunda variable y dividiendo entre el producto de las desviaciones estandar y los grados de libertad. Llamemos las variables y . El coeficiente de Pearson es:
Correlación entre diferentes variables de la ECV
En el texto de Chen1 se incluyen dos preguntas relacionadas con la correlación entre las variables.
Para llevar a cabo el análisis, construimos un DataFrame que incluya
variables de las categorías educación y salud de la encuesta
calidad de vida. La fuente de datos está en
https://microdatos.dane.gov.co/index.php/catalog/827/get-microdata.
Se cargan los datos:
educacion = pd.read_csv('Educación.CSV',sep=';',usecols=['DIRECTORIO','SECUENCIA_P','SECUENCIA_ENCUESTA','P8587','P6216','P6167'])
salud = pd.read_csv('Salud_ajustada/Salud.CSV',sep=';',usecols=['DIRECTORIO','SECUENCIA_P','SECUENCIA_ENCUESTA','P6181','P6127'])
Aquí es necesario hacer un análisis cuantitativo de las variables de
cada DataFrame. La variable P6181 es ‘la calidad de servicio de las
EPS’, en escala desde 1: ‘muy buena’ hasta 5 ‘muy mala’ y 5 ‘no
sabe’. La variable P6127 es ‘el estado de salud’, en escala desde 1
‘Muy Bueno’ hasta 4 ‘Malo’.
print(salud.describe())
DIRECTORIO SECUENCIA_ENCUESTA SECUENCIA_P P6181 P6127
count 2.402120e+05 240212.000000 240212.000000 230206.000000 240212.000000
mean 8.031243e+06 2.296455 1.004138 2.256457 1.999546
std 9.681928e+04 1.404147 0.071554 1.081347 0.560144
min 7.910114e+06 1.000000 1.000000 1.000000 1.000000
25% 7.948281e+06 1.000000 1.000000 2.000000 2.000000
50% 7.993168e+06 2.000000 1.000000 2.000000 2.000000
75% 8.162668e+06 3.000000 1.000000 2.000000 2.000000
max 8.201927e+06 24.000000 6.000000 9.000000 4.000000
Aquí encontramos una inconsistencia en la variable P6181, porque el
resumen indica que el valor máximo de la variable es 5, pero aparece
registrado un valor de 9. En este caso podemos hacer un filtro para
remover éstos valores. Primero generamos una nueva variable y luego
procedemos a remover la columna.
salud['P6181f'] = salud.P6181[salud.P6181!=9]
salud = salud.drop(columns=['P6181'])
Queda como tarea a quien está leyendo este texto el hacer un análisis descriptivo siguiendo las etapas que están anteriormente para describir las variables del dataframe de salud y de educación que hemos incluido.
Construimos un DataFrame con las varialbes de ambos DataFrames:
df_es_i = pd.merge(left=educacion,right=salud,how='inner',left_on=["DIRECTORIO",'SECUENCIA_P',"SECUENCIA_ENCUESTA"], right_on=["DIRECTORIO",'SECUENCIA_P',"SECUENCIA_ENCUESTA"])
Las tres primeras variables corresponden a la identificación de los registros, por lo tanto no es necesario incluirlas en el análisis de correlación.
dfsinetiquetas = df.drop(columns=['DIRECTORIO','SECUENCIA_ENCUESTA', 'SECUENCIA_P'])
En Pandas se incluye la función corr, que permite calcular
diferentes tipos de correlación. Para construir la gráfica de la
correlación, usamos las siguientes instrucciones:
plt.figure()
plt.title("Correlación")
sns.heatmap(dfsinetiquetas.corr(), vmin=-1, vmax=1,cmap=sns.diverging_palette(20, 220, as_cmap=True))
plt.savefig("correlacion.png")
Lo que nos genera la siguiente gráfica:
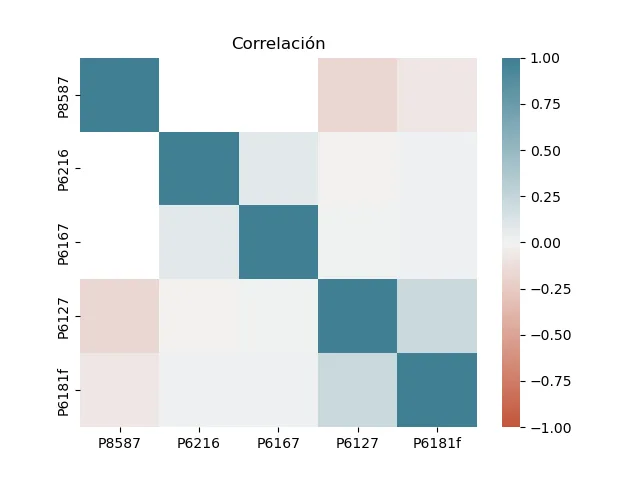
El texto de Chen1 propone dos preguntas sobre la correlación. La primera:
| Fase | Preguntas comunes | Análisis |
|---|---|---|
| Identificación de variables importantes | ¿Hay variables correlacionadas? | Se encuentra una correlación positiva entre la variable P6127, “el estado de salud en general” y P6181, “la calidad del servicio de la EPS”. |
| Fase | Preguntas comunes | Análisis |
|---|---|---|
| Identificación de variables importantes | ¿Se puede hacer una modificación para mejorar la correlación? |
Cruzar variables
los diferentes censos. ¿qué dice un análisis exploratorio de las variables ‘Edad’ y ‘Lugar de Residencia hace 5 años’ de la categoría personas?
Falacia de Causa Simple10
Pensemos en la siguiente situación. Supongamos que usted tiene tomates de dos colores diferentes, naranja y rojo, y quiere analizar si existen diferencias significativas en el contenido nutricional de los tomates con respecto a su color.
Entonces usted lleva a cabo un experimento, en el que toma 100 tomates rojos y 100 tomates de color naranja y les mide su contenido nutricional. Promedia en cada muestra y obtiene que los tomates rojos tienen un contenido nutricional mayor al de los tomates naranja. Usted concluye que el color en tomates se correlaciona con el contenido nutricional.
Ahora, al exponer sus resultados, sus pares le hacen las siguientes preguntas:
-
¿ambos colores de tomate (rojos y naranja) tenían del mismo tiempo de maduración?
-
¿ambos colores de tomate (rojos y naranja) eran del tamaños similares?
Usted revisa sus datos y encuentra que efectivamente los tomates tenían todos el mismo tiempo de maduración, sin importar el color. Pero luego revisa el tamaño y encuentra que entre los tomates naranja había una mayor fracción de tomates pequeños que en los tomates rojos. Cuando usted compara el contenido nutricional teniendo en cuenta el tamaño halla que claramente los tomates grandes son más nutritivos que los pequeños. Su tarea ahora es repetir el experimento inicial (del color), garantizando que en ambos grupos hay una distribución similar de tamaños.
Comunmente nos interesa analizar cuáles son los valores de los estadísticos de centro de una variable (cuantitativa), al filtrar por una segunda variable (categórica). Un caso común pasa cuando se plican diferentes tratamientos en un proceso y se busca saber cuál de los tratamientos es el más efectivo. En ese caso se construyen promedios de la variable de estudio filtrando por la variable de tratamiento.
Este análisis se comienza teniendo en cuenta una única variable de filtro (categórica, que representa el tratamiento) a la vez. Si sólo tenemos una variable categórica, o si tenemos varias variables categóricas pero están igualmente distribuidas, el procedimiento no es problemático. En el caso contrario podemos llegar a un error. Este error se conoce como la Falacia de Causa Simple, o también como Paradoja de Simpson.
Vemos un ejemplo en las estadísticas vitales del Dane en el caso de los nacimientos11. Comenzamos por cargar los datos, e imprimir la lista de las variables:
datos = pd.read_csv("Nacimientos_1998.txt",encoding="ISO-8859-1", sep="\t")
print(datos.columns)
Nos interesa saber cómo cambia la distribución del peso al nacer de
los neonatos con respecto a las diferentes variables. En la
descripción de la variable peso_nac, encontramos que no se registró
el valor del peso, en su lugar se codificó de la siguiente manera:
Peso del nacido vivo, al nacer
1. Menos de 1.000
2. 1.000 - 1.499
3. 1.500 - 1.999
4. 2.000 - 2499
5. 2.500 - 2.999
6. 3.000 - 3499
7. 3.500 - 3.999
8. 4.000 y más
9. Sin información
Podemos hacer un promedio de ésta variable para identificar el rango promedio del peso de neonatos en la base de datos. Sin embargo estaríamos cometiendo un error, dado que los valores correspondientes al 9 incrementarían el promedio, cuando en realidad son valores faltantes; de nonatos que podrían tener un bajo peso.
Por esta razón procedemos a construir una base de datos en la que no se incluyan los registros para los cuales no tenemos el peso del nacido vivo.
dtp = datos[datos.peso_nac!=9]
Ahora queremos averiguar si la variable areanac está relacionada con
el peso. Esta variable identifica el tipo de áreas, entre:
1. Cabecera municipal
2. Centro poblado (Inspección, corregimiento o caserío)
3. Rural disperso
9. Sin información
Entonces construimos una tabla pivote en la que calculamos el promedio del peso para las diferentes áreas:
dtp.groupby('areanac')['peso_nac'].mean()
areanac
1 5.883806
2 6.159185
3 6.181898
9 6.168539
Name: peso_nac, dtype: float64
Encontramos que para la categoría 1, que corresponde a las cabeceras municipales, tenemos un menor promedio de la variable peso al nacer que pra los centros poblados, para rural disperso y para los registros sin información. Este resultado es un poco anti intuitivo, esperaríamos que las zonas rurales y los caseríos tuviesen mayores dificultades en términos de cuidado de neonatos que las cabeceras. ¿que podría estar pasando?
Revisando en las variables encontramos la variable t_ges. Esta
variable identifica el tiempo de gestación del neonato. Aquí entra el
conocimiento disciplinar de la medicina en el análisis. Una revisión
de la literatura nos indica que el tiempo de gestación debe estar
cerca de las 40 semanas, y que a menos tiempo de gestación tendremos
neonatos más bajos de peso.
La variable t_gesse define como:
Tiempo de gestación del nacido vivo
1. Menos de 22
2. De 22 a 27
3. De 28 a 37
4. De 38 a 41
5. De 42 y más
6. Ignorado
9. Sin información
Construímos una tabla entre tiempo de gestación y peso:
dtp.groupby(['t_ges'])['peso_nac'].mean()
t_ges
1 1.019608
2 1.667897
3 4.869444
4 6.030346
5 6.348006
6 5.829720
9 5.904743
Name: peso_nac, dtype: float64
Efectivamente se encuentra que para los neonatos de menos de 22 semanas el peso al nacer es casi la sexta parte del peso de los neonatos que tienen alrededor a 40 semanas. El número de semanas de gestación determina fuertemente el peso al nacer.
Revisamos si hay una fracción mayor de neonatos con menos semanas de
gestación en las cabeceras. Para eso promediamos la variable t_ges
ordenando por la varialbe areanac. Ahora, aquí tenemos que retirar
los datos para los que no tenemos valor de t_ges, que en la base
están registrados con el código 9 y nos desviarían el resultado:
dtp[dtp.t_ges!=9].groupby('areanac')['t_ges'].mean()
areanac
1 3.913313
2 3.964945
3 4.015761
9 4.164557
Name: t_ges, dtype: float64
Efectivamente se encuentra que en promedio el tiempo de gestación es menor en las cabeceras con respecto a las áreas rurales. Esto puede estar incidiendo en el promedio del peso. Tendríamos que construir una muestra en la que se tenga en cuenta esta variable.
Por otro lado es importante analizar las condiciones que no están en los datos. ¿es posible que en las cabeceras haya condiciones que permitan que algunos neonatos que no llegaran a término o que fallecieran en el parto sobrevivan, y por lo tanto al salvarles el promedio es más bajo allí? Estas preguntas deben guiar el proceso de análisis y de recolección de datos.
Correlación y Causalidad12
Es importante recordar que cuando dos variables, digamos la variable A y la variable B están correlacionadas existen varias
posibilidades:
-
Que
variable Asea la causa de lavariable B(o al revés). Por ejemplo: los largos tiempos de espera en atención a usuarios causan molestias e inconformidades en la prestación del servicio. -
Que
variable Asea la causa de lavariable B, pero a su vez lavariable Btambién cause lavariable A. Por ejemplo, la enfermedad dental puede llevar a dificultades de nutrición. Pero problmeas de nutrición pueden llevar a enfermedad dental. -
Que tanto la
variable Acomo lavariable Bsean causadas por otravariable C. Por ejemplo en un entorno educativo los problemas de comportamiento y las bajas notas pueden ser causadas a su vez por situaciones personales subyacentes. -
Que no haya relación alguna entre las dos variables. Por ejemplo la variable
películas con Nicholas CageyPersonas ahogadas en una piscinaestán correlacionadas. Pero no hay ninguna relación entre estas dos variables 13.
Es decir, correlaciòn no implica causalidad, pero cuando si hay causalidad se hallará correlaciòn
Inferencia Causal14
Para determinar si la variable A causa el efecto B, se define una
serie de condiciones:
-
Correlación. Discutido en la sección anterior.
-
Precedencia Temporal. Para que
AcauseBtiene que haber ocurrido antes. -
Eliminación de variables de confusión. Como vimos antes, hay que revisar si hay alguna otra variable que sea la verdadera causa.
Como menciona Chen et al., un ejemplo de éste procedimiento ocurre en los estudios de eficacia de medicinas. Se analiza cómo diferentes tratamientos se correlacionan con el resultado, para asegurar que la correlación existe y para determinar bajo que condiciones es más fuerte. Se tiene un conocimiento disciplinar sobre el tiempo de metabolización del compuesto, o del efecto biológico de la vacuna, lo que guía los análisis temporales. Finalmente se diseña el experimento teniendo en cuenta las variables de la población, de tal forma que se pueda eliminar variables de confusión que puedan afectar las conclusiones.
Inferencia
La investigación aplicada en ciencias sociales busca responder preguntas sobre problemas reales, utilizando el conocimiento de las diferentes disciplinas. En el caso de los métodos cuantitativos una de éstas disciplinas es la estadística, y una de las formas en que se utiliza es mediante el diseño de experimentos.
Diseño de experimentos15
Se comienza por formular una hipótesis, que será una relación entre las variables de estudio. Para tener evidencia que la sustente o la refute se diseña un experimento. Al aplicar este experimento a una muestra de la población se obtendrán datos. Estos se anlizan para inferir conclusiones, lo que nos puede llevar a replantear las hipótesis.
Prueba AB
Son los experimentos en los que hay dos tratamientos, llamados
tratamiento A y tratamiento B. También se refieren a ellos como
intervenciones, se trata del proceso de someter a los sujetos de
estudio a un proceso. Usualmente uno de ellos es el tratamiento
estándar, o control, y el otro el grupo de tratamiento.
Una posible discusión es cómo se ve afectada la productividad al
incluir días de trabajo en casa. Para analizarlo se diseñaría un
experimento en el que se mediría la productividad para dos grupos. El
tratamiento A, o tratamiento estandar, correspondería a un grupo al
cual no se le modifica la modalidad de trabajo, es decir, no tienen
trabajo en casa. Al tratamiento B sería un grupo al que se le
incluye un día de trabajo en casa.
En la siguiente etapa se lleva a cabo un análisis estadístico, dependiendo del problema a tratar. Por ejemplo, puede ser:
Ejemplo
TODO: Revisar. Hay uno en la página 90 de Data Science from Scratch
Prueba de Hipótesis Estadística17
En las pruebas de hipótesis o de significancia se busca deterinar si existe evidencia de que un efecto puede ser resultado de una intervención. Para esto se comparan la probabilidad de obtener un resultado dado de un experimento con la de que este mismo resultado ocurra de forma totalmente aleatoria.
Como ejemplo pensemos en un proceso de producción agrícola, que tiene un proceso estandarizado bajo el que se genera una productividad dada. Ahora ese nivel de productividad tiene una variabilidad, aplicando el mismmo proceso a veces tenemos una producción más alta. Pero se sabe que es muy poco probable que la productividad se duplique, de hecho nunca ha pasado. Una prueba de hipótesis estadística nos cuantifica en qué casos podemos decir que tenemos evidencia de que un tratamiento diferente realmente puede haber afectado la productividad.
-
Hipótesis nula
-
Hipótesis alternativa
TODO: revisar el libro de contento y ver como lo hacemos aquí en Python
Estimación puntual
El uso de una estadística para estimar, o hallar un valor cercano al valor real, de un parámetro. Ejemplo: Uso del promedio muestral , para acercarnos al promedio poblacional .
Intervalo de Confianza
Intervalo en el cual esperamos que esté el valor del parámetro con una confiabilidad pre-establecida.
Distribución de Muestreo
Distribución de probabilidad de una estadística basada en muestras aleatorias.
Estimación por intervalo
Para una variable aleatoria . Queremos estimar un parámetro. ¿cómo sabemos en que rango de valores estará el parámetro? Queremos tener:
- Alta confiabilidad : que el parámetro muy seguramente esté en el intervalo.
- Intervalos angostos
- No conocemos los parámetros (, )
- Podemos estimar en muestras (, )
- Sabemos el tamaño de la muestra, .
Intervalo de Confianza para
(La fórmula se desarrolla en Contento 2019, pg. 274 )
Una agencia ambiental mide el promedio de masa () en 1 de aire. Toma Si hay mediciones, y obtiene los valores: 58, 70, 57, 61 y 59. Es decir tiene un , y , ¿cuál es el intervalo de confianza del 95% ?
-
es una distribución t-student con grados de libertad.
-
es la probabilidad a cola derecha.
-
Para calcularla en python:
-
Se usa la librería
scipy.statsy de allí se calcula con la funciónt.ppf. -
Los argumentos de la función son y los grados de libertad
-
Por ejemplo, se calcula , para y , así:
from scipy.stats import t t.ppf(1-0.05,10)y si lo queremos usar después se puede asignar el valor a una variable.
-
Ejemplo18
Una agencia ambiental mide el promedio de masa () en 1 de aire. Toma Si hay mediciones, y obtiene los valores: 58, 70, 57, 61 y 59. Es decir tiene un , y , ¿cuál es el intervalo de confianza del 95% ?
Respuesta
Llamamos librerías:
import scipy.stats as st
import numpy as np
import pandas as pd
Calculamos el promedio y la desviacion estandar:
valores = np.array([58,70,57,61,59])
promedio = valores.mean()
S = st.tstd(valores)
Como queremos que la confianza sea del 95%, entonces tenemos que:
Esto quiere decir que y por lo tanto
Como son 5 mediciones, tenemos que
Con estos datos calculamos la distribución :
se calcula así:
from scipy.stats import t
t.ppf(1-0.025,4)
Como queremos usar el valor después, por precisión, podemos asignar a una variable:
t0=t.ppf(1-0.025,4)
Los valores de los extremos izquierdo y derecho serán:
Que siguiendo lo que hicimos, en el software se calcula como:
li = promedio - t0*S/np.sqrt(5)
ld = promedio + t0*S/np.sqrt(5)
print(li,ld)
Ahora si podemos aproximar a dos decimales.
El intervalo sería, entonces: (54.49,67.51)
Hipótesis estadística y evidencia
Pongamos el siguiente ejemplo del campo de la epidemiología. Suponga que surge una nueva enfermedad que anteriormente no existía en Colombia, pero de la que ya hay casos en otros países. Para identificar si la enfermedad ya llegó al país, la autoridad de salud decide hacer un tamizaje, es decir, toma una muestra de la población y le hace un examen para identificar si están o contagiados.
Ahora, aquí hay una sutileza en el argumetno estadístico. Cada vez que no econtramos personas contagiadas no tenemos evidencia de que la enfermedad ha llegado al país. Pero esto puede ser porque realmente no ha llegado, o que ya llegó y simplemente por azar las muestras que hemos tomado no incluyen a nadie enfermo. Dicho de otra forma, la falta de evidencia de un hecho positivo no es en sí evidencia de un hecho negativo.
Es decir, en este caso (tomando muestras) sólo podemos probar que la enfermedad llegó; no podemos probar que la enfermedad no ha llegado.
p-Hacking (DSS)
La situación del apartado anterior se complica en el caso de que las pruebas que realizamos tienen una probabilidad de fallo. Supongamos que tenemos una tasa de falsos positivos del 5%. Si simplemente queremos encontrar una prueba marcada positiva, podemos repetir la prueba hasta que el resultado sea positivo. Como las pruebas tienen una fracción de falsos positivos, en algun momento tendrá que marcar como positivo. Esto se conoce como p-hacking.
Otra mala práctica relacionada con el p-Hacking es la siguiente. Si se tienen los resultados de la medición de diferentes variables, se pueden en teoria hacer análisis que busquen encontrar una relación significativa entre todas ellas. De nuevo, si se hacen suficientes ensayos es posible que en uno de ellos se encuentre una correlación, así sea por falsos positivos.
Ejemplo, simulación de p-Hacking19
Supongamos que un experimento puede tener sólo dos opciones. En el campo público puede ser:
-
Identificar si una persona ha recibido una dosis de una vacuna o no.
-
Identificar si una persona está recibiendo educación o no.
Si la probabilidad de que una persona elegida al azar cumpla con la característica es del 0.5, entonces podríamos simular el proceso utilizando un generador aleatorio.
Aquí está la En Python esto se haría de la siguiente forma.
Vemos la forma de programarlo y su interpretación en términos del experimento social:
| Etapa del experimento | Simulación en Python |
|---|---|
| Identificar si una persona tiene la característica | random.choice([0,1]) |
| Identificar si 1000 personas tienen la característica | [random.choice([0,1]) for i in range(1000)] |
| Identificar cuántas personas tienen la característica | sum([random.choice([0,1]) for i in range(1000)]) |
Es decir, sería el siguiente código:
import random
nexitos = sum([random.choice([0,1]) for i in range(1000)])
Esta instrucción construye una lista con valores Truey False, que
tienen una distribución uniforme con ambos valores igual de probables,
calcula el número de éxitos y lo guarda en la variable
nexitos. Ahora:
-
Cada uso de la instrucción representa una muestra aleatoria
-
Estas muestras tendrán diferentes número de éxitos es decir de valores de
True -
El teorema del límite central nos dice que el promedio de las sumas es un valor muy cercano a , es decir
-
Es raro pero posible encontrar muestras cuya suma esté lejos de 500.
Ahora podríamos construir un intervalo de confianza para la variable
número_de_éxitos. Como , la hipótesis nula es que
. Definiendo un valor de significancia
del 5%, llegamos a un intervalo de confianza para el número de éxitos
en el rango . Este intervalo de confianza se interpreta de
la siguiente forma. Si tomamos una muestra y esta tiene una fracción
de éxitos por fuera de éste rango, tendríamos evidencia contra la
hipótesis nula.
El p-hacking sería repetir el experimento muchas veces, hasta encontrar una muestra cuyo número de éxitos esté por fuera del intervalo de confianza. Sabemos que es posible, aunque raro, que esto pase. Veamos:
parar = False
maxrep = 5000
i=0
while parar == False:
i=i+1
nexitos = sum([random.choice([0,1]) for i in range(1000)])
if (nexitos<469 or nexitos>531):
print(" la muestra " + str(i) + " tiene un número de éxitos fuera del rango")
parar=True
if i==maxrep:
print("En "+str(maxrep)+" muestras ninguna cae fuera del rango")
parar=True
La estructura while repetirá un bloque de instrucciones, mientras
que la variable parar sea False. La primera instrucción es contar
cuantas veces se ha repetido el proceso. La segunda instrucción toma
una muestra y suma el número de aciertos. Luego, si el número de
éxitos cae por fuera del intervalo de confianza imprimmos el número de
la muestra y el número de éxitos y hacemos la variable pararigual al
valor True. Luego hay un bloque que, si se llega a un valor máximo
de repeticiones hace que la variable parar sea True e imprime a
pantalla.
Si usted ejecuta el código varias veces verá que se encuentra una muestra por fuera del intervalo de confianza relativamente rápido.
Inferencia Bayesiana (DSS)
Creo que esto ya es demasiado avanzado para nuestra población
ANOVA (PSDS)
Comparaciones de varios tratamientos.
Supongamos que tenemos tres o más tratamientos para comparar y queremos saber cuál de ellos es el mejor. Por ejemplo supongamos que hay una infestación que afecta a la población de árboles de una región. En un análisis disciplinar se determinó cuál es el compuesto que se puede usar para tratar los árboles, pero tenemos dos fuentes de variación:
-
Se puede administrar el compuesto en diferentes concentraciones, disuelto en 1 l de agua o en 2 l de agua.
-
Se pueden administrar en diferentes cantidades, digamos 10 ml o 5 ml.
En principio lo más sencillo logísticamente sería aplicar la menor dosis en cantidad y menos diluida. Pero eso no quiere decir que sea la más útil.
Para definir cuál es la mejor forma de aplicar el compuesto podemos hacer comparaciones apareadas (A/B). Pero como serían varias podríamos caer en un proceso de p-Hacking.
Características de ANOVA
El acrónimo en inglés de análisis de variaciones (ANalysis Of VAriations) compara los grupos analizando dos formas de la varianza. Por un lado está la varianza interna de cada tratamiento y por otro lado la varianza entre los diferentes tratamientos.
En el caso en que tengamos tres o más tratamienos para comparar no es buena idea hacer comparaciones A/B, por varias razones, entre ellas la probabilidad de que al hacer varias comparaciones podamos encontrar correlaicones espúreas (p-hacking).
Para hacerlo, el método compara dos tipos de variación.
-
La varianza dentro de los grupos, es decir, que tanto varían los datos dentro del mismo grupo. Por ejemplo sería la variación de los cuadrados azules con respecto a su promedio.
-
La varianza entre grupos, es decir la comparación entre un grupo con respecto al otro. Por ejemplo, los promedios de los discos cuadrados con respecto al promedio de los triángulos rojos.
-
La variación total (suma de cuadrados total) es igual a sumar la suma de cuadrados entre tratamientos más la suma de cuadrados dentro de los tratamientos.
-
Los cuadrados medios se calculan al dividir cada suma de cuadrados entre los grados de libertad.
La descripción de éste método se trata a profundidad en diferentes textos20. Se trata de un experimento estadístico, que tiene las siguietnes características:
- La hipótesis nula es que los promedios entre los grupos son similares, y por lo tanto la variación entre grupos es similar a la variación dentro de los grupos.
- La hipótesis alternativa es que hay un promedio diferente. Esto lleva a que la variación entre grupos es mayor a la variación dentro de los grupos.
-
Debemos indicar el nivel de significancia con el que consideramos que hay evidencia suficiente contra la hipótesis alternativa, es decir, tenemos inferencia de que hay un grupo diferente. Por ejemplo un nivel de significancia del 5%, o 0.05.
-
El software produce un valor-p, que se puede comparar contra el nivel de significancia para determinar si concluimos que hay evidencia de que uno de los grupos es diferente.
Implementación en Python
Para implementar Anova en Python se usa la librería statsmodels:
import statsmodels.formula.api as smf
import statsmodels.api as sm
Como ejemplo tomemos el experimento del efecto de la nutrición sobre los niveles de atención de los alumnos de primaria que menciona Contento21. Se quiere determinar si tres tratamientos, sin desayuno, desayuno ligero y desayuno completo, tienen un efecto en los tiempos de atención a lectura.
Los datos son los siguientes:
tiempos = [8,7,9,13,10,14,16,12,17,11,10,12,16,15,12]
niveles = ["ND","ND","ND","ND","ND","DL","DL","DL","DL","DL","DC","DC","DC","DC","DC"]
Las etiquetas representan: No desayuno, ND; Desayuno ligero, DL;
Desayuno Completo, DC y los tiempos de lectura correspondientes (por
ejempo 8, 7, 9 corresponden a ND, y los valores 16,15,12 a DC)
Ahora construimos un DataFrame con esta información, y lo imprimimos.
df = pd.DataFrame({'tiempos':tiempos, 'niveles':niveles})
print(df)
Definimos que queremos construir un modelo de ajuste que tome como variable dependiente los tiempos y los categorice según los niveles. Y procedemos a aplicar el analisis de varianza (aquí AOV):
model=smf.ols('tiempos ~ niveles', data=df).fit()
aov_table=sm.stats.anova_lm(model)
Imprimimos los resultados del análisis:
print(aov_table)
Lo que produce la siguiente tabla:
df sum_sq mean_sq F PR(>F)
niveles 2.0 58.533333 29.266667 4.932584 0.027326
Residual 12.0 71.200000 5.933333 NaN NaN
Aquí se calculan los cuadrados medios y la variable F20. El valor-p en este caso es 0.027326. Como es menor a 0.05, “se puede concluir que al nivel de confianza del 5% hay evidencia para pensar que al menos con uno de los tres tipos de desayuno se obtiene un tiempo promedio de atención diferente”22.
Regresión
En un experimento se tiene una variable explicativa (o independiente) y una variable de respuesta (o dependiente). El análisis de regresión supone una relación lineal entre esas dos variables, y busca cuantificar esa relación.
Regresión Lineal Simple
Modelo
Es el siguiente:
Que se interpreta como:
-
, es una aproximación lineal, con el intercepto con y la pendiente)
-
es la distancia entre el valor y el modelo, también llamada error o residual.
Por ejemplo en la siguiente gráfica los datos están marcados con cuadrados azules, la aproximación lineal por círculos verdes. Las líneas verticales representan la diferencia o distancia entre los dos valores 23.
Ejemplo: indicadores de gobernanza global
El banco mundial ha desarrollado una base de datos llamada Worldwide Governance Indicators, donde busca resumir la calidad del gobierno en varios países del mundo. Después de descargar la base de datos24, se obtiene un archivo en formato propietario de Microsoft Excel.
Para cargarlo a Python hacemos lo siguiente. Primero cargamos las librerias pandas y numpy.
import pandas as pd
import numpy as np
Luego procedemos a usar read_excel para cargar los datos:
wgi_df = pd.read_excel("Worldwide Governance Indicators 2012-2022.xlsx")
Como siempre, podemos revisar las variables que se encuentran en el archivo y comparar con la descripción que hacen los autores del mismo conjunto de datos.
print(wgi_df.columns)
Esto devuelve el arreglo Index(['Country ', 'ISO3', 'ID Data', 'Year', 'Voice and Accountability', 'Political Stability', 'Government Effectiveness', 'Regulatory Quality', 'Rule of Law', 'Control of Corruption', 'Region'], dtype='object'). Intentaremos cuantificar la relación entre las variables Regulatory Quality y Government Efficiency. Primero cargamos la librería matplotlib y agregamos título.
import matplotlib.pyplot as plt
plt.ion()
plt.figure()
plt.show()
plt.title("Correlación de indicadores de gobernanza global")
plt.xlabel("Calidad regulatoria")
plt.ylabel("Efectividad del gobierno")
Ahora hacemos un diagrama de dispersión de los valores de las dos variables.
plt.plot(wgi_df['Regulatory Quality'],wgi_df['Government Effectiveness'],'.')
Pareciera que al aumentar la variable Regulatory Quality hay valores
mayores en Government Effectiveness. Para cuantificar ésta relación
proponemos un análisis de regresión lineal. Primero importamos la
función linear_model de la librería sklearn, y creamos un modelo lineal.
from sklearn import linear_model
reg = linear_model.LinearRegression()
Para poder usar el ajuste requerimos que los datos independientes
estén organizados de una forma particular. Primero los cargamos en el
arreglo rq de Python, y luego los reorgamizamos.
rq = np.array(wgi_df['Regulatory Quality'])
rq=rq.reshape(-1,1)
Ahora si podemos hacer el ajuste, con el comando fit. Recibe como
argumentos el arreglo correspondiente a la variable independiente que
habíamos generado atrás y el vector de la variable dependiente. Luego
procedemos a graficarlo y grabar la figura.
reg.fit(rq,np.array(wgi_df['Government Effectiveness']))
plt.plot(rq,reg.predict(rq),linewidth=2,color="orange")
plt.savefig('wgi_reg.svg')
Los residuales se pueden calcular mediante la diferencia
entre los valores de la variable Government Effectiveness y el valor por el modelo:
residuals = wgi_df['Government Effectiveness'] - reg.predict(rq)
Podemos hacer un histograma de residuales.
plt.figure()
plt.title("Histograma de residuales de la \n Correlación de indicadores de gobernanza global")
plt.hist(residuals)
Los parámetros de la recta son su pendiente y el intercepto con el
eje. Se obtienen respectivamente con coef_ e intercept:
print("la pendiente es " + str(reg.coef_))
print("el intercepto es " + str(reg.intercept_))
Puede encontrar más información sobre la regresión lineal en las referencias25.
Regresión Múltiple26
En el modelo de regresión lineal simple, tenemos sólo una variable explicativa y una variable de respuesta. En la regresión múltiple hay más de una variable explicativa. En general, si son variables explicativas:
donde define cada uno de los datos a ajustar,
Por ejemplo, para el caso de dos variables explicativas:
Aquí
-
, es una aproximación lineal, con el intercepto con y los demás valores de son las pendientes)
-
es la distancia entre el valor y el modelo, también llamada error o residual.
Si son dos variables explicativas, la aproximación lineal es un plano.
Ejemplo
Volvemos a los Worldwide Governance Indicators del Banco Mundial. Si
podemos tomar como variables explicativas a : Voice and Accountability y Regulatory Quality y como variable depdendiente a
Government Effectiveness, tendríamos el siguiente procedimiento.
Inicialmente cargamos las librerías y cerramos las gráficas:
import pandas as pd
from sklearn import linear_model
from sklearn.metrics import mean_squared_error
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
plt.close('all')
Ahora definimos los predictores y el modelo lineal:
predictors=['Voice and Accountability','Regulatory Quality']
outcome = 'Government Effectiveness'
lm = linear_model.LinearRegression()
Leemos los datos:
wgi_df = pd.read_excel("Worldwide Governance Indicators 2012-2022.xlsx")
La función fit hace el ajuste, toma como argumentos los nombres de
las variables, predictores y de la variable objetivo.
lm.fit(wgi_df[predictors],wgi_df[outcome])
Aquí podemos generar un resumen del ajuste. Para esto usamos la
librería sklearn. Primero generamos un modelo, y hacemos el
ajuste. Luego imprimimos los resultados de éste proceso.
model = sm.OLS(wgi_df[outcome], wgi_df[predictors].assign(const=1))
results = model.fit()
print(results.summary())
Los resultados del análisis son:
OLS Regression Results
====================================================================================
Dep. Variable: Government Effectiveness R-squared: 0.860
Model: OLS Adj. R-squared: 0.860
Method: Least Squares F-statistic: 6093.
Date: jue, 10 abr 2025 Prob (F-statistic): 0.00
Time: 13:47:39 Log-Likelihood: -7520.6
No. Observations: 1980 AIC: 1.505e+04
Df Residuals: 1977 BIC: 1.506e+04
Df Model: 2
Covariance Type: nonrobust
============================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------------
Voice and Accountability 0.0332 0.014 2.392 0.017 0.006 0.060
Regulatory Quality 0.8983 0.014 65.642 0.000 0.871 0.925
const 2.8740 0.486 5.918 0.000 1.922 3.826
==============================================================================
Omnibus: 177.632 Durbin-Watson: 0.341
Prob(Omnibus): 0.000 Jarque-Bera (JB): 363.095
Skew: 0.576 Prob(JB): 1.43e-79
Kurtosis: 4.753 Cond. No. 154.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Tenemos un valor de , que es cercano a 1.
Para generar la gráfica cargamos la figura y generamos un eje con
proyección 3D27. El comando scatter genera el diagrama de
dispersión. Y el comando set_xlabel genera la etiqueta del eje x.
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(wgi_df['Voice and Accountability'],wgi_df['Regulatory Quality'],wgi_df['Government Effectiveness'], marker='o')
Para generar una gráfica del plano construimos las variables que
varíen en los mismos rangos de las variables. Generamos una malla con
esos valores de los variables. Y procedemos a generar un plano con las
constantes de ajuste del modelo lm. Generamos el plano con el
comando plot_surface, y grabamos con savefig 28.
x=np.linspace(0,100,100)
y=np.linspace(0,100,100)
x, y = np.meshgrid(x, y)
plano = x * lm.coef_[0] + y * lm.coef_[1]
ax.plot_surface(x,y,plano,alpha=0.4)
plt.show()
plt.savefig('3dfitwgi.svg')
En la interfaz de Python se puede mover la figura para mejorar la visualización.
Regresión de funciones no lineales29
En los dos casos anteriores ha habido una relación lineal entre variables explicativas y variables de respuesta. En los casos en los que la relación no es lineal se pueden usar los procedimientos de Regresión, pero es necesario primero llevar a cabo una transformación de los datos.
Veámos un ejemplo. Iniciamos cargando librerías y generando la figura.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.ion()
plt.close('all')
fig = plt.figure()
ax = plt.gca()
Aqui usted cargaría sus datos. Para este ejemplo propongo usemos los siguientes arreglos de datos:
x=[2.91915403e+00, 5.04227145e+00, 8.00623721e-04, 2.11632801e+00,
1.02729124e+00, 6.46370163e-01, 1.30382148e+00, 2.41892509e+00,
2.77737232e+00, 3.77171714e+00, 2.93436160e+00, 4.79653650e+00,
1.43116575e+00, 6.14682205e+00, 1.91713152e-01, 4.69327257e+00,
2.92113362e+00, 3.91082880e+00, 9.82708570e-01, 1.38671042e+00,
5.60521198e+00, 6.77783103e+00, 2.19396925e+00, 4.84625831e+00,
6.13472407e+00, 6.26224664e+00, 5.95309480e-01, 2.73383483e-01,
1.18881294e+00, 6.14699752e+00, 6.88427837e-01, 2.94775338e+00,
6.70522671e+00, 3.73215699e+00, 4.84313980e+00, 2.20860942e+00,
4.80550649e+00, 5.84237970e+00, 1.28017941e-01, 5.25101020e+00,
6.92202762e+00, 5.23715958e+00, 1.96310794e+00, 5.52495530e+00,
7.22582046e-01, 3.13525468e+00, 6.36016852e+00, 2.05529904e+00,
2.01442737e+00, 9.10200005e-01]
y=[ 0.15189155, -1.03060098, -0.06632399, 0.85358508, 0.74417029,
0.62573434, 1.13055361, 0.73559223, 0.33703733, -0.67800824,
0.13103516, -0.82721623, 0.99534825, -0.1996406 , 0.20963249,
-0.78979177, 0.23069347, -0.63386635, 0.86202009, 0.947879 ,
-0.74146767, 0.4397856 , 0.79114136, -0.93239056, -0.06401813,
0.07217308, 0.58932376, 0.35850492, 0.85248734, -0.01048038,
0.68661685, 0.1628184 , 0.4584754 , -0.56438704, -0.87830134,
0.95538153, -0.77711016, -0.56631783, -0.01674283, -0.90886333,
0.61227017, -0.777822 , 0.95559123, -0.88985753, 0.63070327,
0.08913539, 0.09991667, 0.9611078 , 0.88096628, 0.76955067]
Tenemos una variable explicativa y una variable de respuesta . El diagrama de dispersión resulta ser el siguiente:
plt.plot(x,y,'.',label='datos')
Una aproximación lineal simple seguiría el modelo:
Pero esto correspondería a una recta, que claramente no se ajusta a los datos. Una aproximación lineal múltiple seguiría el modelo:
La estrategia consiste en llevar a cabo transformaciones no lineales (polinomiales o trascendentes) de la variable . En este caso, si usamos:
Obtendríamos:
De esta forma se usa el modelo lineal para encontrar los coeficientes . Una forma de hacer éste proceso de manera eficiente es la siguiente. Primero cargamos librerías:
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
Ahora definimos la transformación polinomial. En este caso el númro 3 indica que vamos hasta potencias al cubo.
from sklearn.pipeline import make_pipeline
poly_model = make_pipeline(PolynomialFeatures(3), LinearRegression())
Ahora hacemos el ajuste al modelo y generamos los datos de la
predicción. Primero construimos un vector ordenado que tenga valores
extremos (mínimo y máximo) similares a los de la variable . Ese
arreglo lo llamamos xfit. Luego hacemos una predicción, es decir
, usando el modelo polinomial que habíamos
construido. Finalmente graficamos el ajuste e imprimimos la leyenda.
xfit = np.linspace(0,7,50)
yfit = poly_model.predict(xfit[:, np.newaxis])
plt.plot(xfit,yfit,'g-',label='ajuste cúbico')
plt.legend()
A manera de cierre
Hasta aquí la presentación de algunas herramientas de ciencia de datos para la administración pública. Se han tratado los temas más importantes, usando una varidedad de ejemplos, de datos reales de Colombia, de datos generados por otras fuentes así como de simulación. A partir de aquí usted puede comenzar a desarrollar nuevos análisis. Recuerde siempre que éstas herramientas son útiles al ser usadas en contexto, incluyendo el análisis disciplinar.
Temas avanzados
En una revisión más a profundidad se pueden tratar temas como:
- Regresión logística
- Regresión Discontinua30
Bibliografía
- Python Data Science Handbook. Jake VanderPlas. O’Reilly. 2023
- R for Data Science. https://r4ds.hadley.nz/
- Representing text as data. https://uclspp.github.io/PUBL0099/seminars/seminar1.html
- Statistical Inference via Data Science. https://moderndive.com/v2/sampling.html
- Data Science for Public Policy. Chen, Rubin, Cornwall. Springer Nature Switzerland AG. 2021
- Practical Statistics for Data Science. Bruce, Bruce, Gedeck.
- Data Science from Scratch, first principles with Python. Second Edition. Joel Grus. O’Reilly. 2019.
- Microdatos DANE, Censo Nacional de Población y Vivienda 2018, Módulo Personas, Región Cundinamarca. https://microdatos.dane.gov.co/index.php/catalog/643/get-microdata
- Microdatos DANE, Censo Nacional de Población y Vivienda 2018, Diccionario de Datos. https://microdatos.dane.gov.co/index.php/catalog/643/data-dictionary/F11?file_name=PERSONAS
- Dir Datos
/home/gavox/drive/02_Docencia/15_ESAP/06_2024_s1/17_map_mcpi/03_TALLERES/TALLER_1_2024_MCPI/03_YUDY - https://python-graph-gallery.com/density-plot/
- OpenIntro Statistics. Fourth Edition. David Diez
- Manuel Ricardo Contento Rubio. Estadística con Aplicaciones en R. Editorial UTADEO. 2010. https://www.utadeo.edu.co/es/publicacion/libro/editorial/235/estadistica-con-aplicaciones-en-r
- Sofik Handoyo, Worldwide governance indicators: Cross country data set 2012–2022, Data in Brief, Volume 51, 2023, 109814, ISSN 2352-3409, https://doi.org/10.1016/j.dib.2023.109814.
Footnotes
-
Dane, https://microdatos.dane.gov.co/index.php/catalog/827 ↩
-
https://microdatos.dane.gov.co/index.php/catalog/827/study-description ↩ ↩2
-
https://microdatos.dane.gov.co/index.php/catalog/827/get-microdata ↩
-
También se puede revisar usando el comando
headde la terminal, en entornos Linux o MacOS X. ↩ -
La bibliografía para ésta sección es: Data Science for Public Policy. Chen, Rubin, Cornwall. ↩
-
En inglés se conoce como Skewed Variables. La bibliografía de ésta sección es: Data Science for Public Policy. Chen, Rubin, Cornwall. ↩
-
La bibliografía para esta sección es: Data Science from Scratch, first principles with Python.Joel Grus; Practical Statistics for Data Science. Bruce, Bruce, Gedeck; OpenIntro Statistics. Fourth Edition. David Diez ↩
-
En inglés se conoce como Paradoja de Simpson. La bibliografía de ésta sección es: Data Science from Scratch. Grus. ↩
-
https://microdatos.dane.gov.co/index.php/catalog/366/data-dictionary/F1?file_name=Nacimientos_1998 ↩
-
La bibliografía para ésta sección es: Data Science for Public Policy. Chen, Rubin, Cornwall. ↩
-
https://www.nationalgeographic.com/science/article/nick-cage-movies-vs-drownings-and-more-strange-but-spurious-correlations visitado el 5 de Abril del 2025. ↩
-
La bibliografía para ésta sección es: Data Science for Public Policy. Chen, Rubin, Cornwall, página 166. ↩
-
La bibliografía para esta sección es: Practical Statistics for Data Science. Bruce, Bruce, Gedeck, página 154. ↩
-
Este tema se trata en los libros estándar de estadística. Por ejemplo, Open Intro Statistics, David Diez, pg. 217. ↩
-
La bibliografía para esta sección es: Practical Statistics for Data Science. Bruce, Bruce, Gedeck, página 164. ↩ ↩2
-
De: Estadística con Aplicaciones en R. Manuel Ricardo Contento Rubio. Editorial UTADEO. 2010. https://www.utadeo.edu.co/es/publicacion/libro/editorial/235/estadistica-con-aplicaciones-en-r, página 275 ↩
-
La bibliografía para esta sección es: Data Science from Scratch, first principles with Python.Joel Grus, página 89. ↩
-
Para comprender a detalle este tema, remitimos a su lectura en los libros estándar de estadística inferencial, como por ejemplo: Estadística con Aplicaciones en R. Manuel Ricardo Contento Rubio. Editorial UTADEO. 2010. https://www.utadeo.edu.co/es/publicacion/libro/editorial/235/estadistica-con-aplicaciones-en-r, página 354 y Open Intro Statistics, David Diez, pg. 285. ↩ ↩2
-
De: Estadística con Aplicaciones en R. Manuel Ricardo Contento Rubio. Editorial UTADEO. 2010. https://www.utadeo.edu.co/es/publicacion/libro/editorial/235/estadistica-con-aplicaciones-en-r, página 362 ↩
-
De: Estadística con Aplicaciones en R. Manuel Ricardo Contento Rubio. Editorial UTADEO. 2010. https://www.utadeo.edu.co/es/publicacion/libro/editorial/235/estadistica-con-aplicaciones-en-r, página 364 ↩
-
Los datos de la gráfica vienen de: Estadística con Aplicaciones en R. Manuel Ricardo Contento Rubio. Editorial UTADEO. 2010. https://www.utadeo.edu.co/es/publicacion/libro/editorial/235/estadistica-con-aplicaciones-en-r, página 368. ↩
-
Handoyo, Worldwide governance indicators: Cross country data set 2012–2022, Data in Brief, Volume 51, 2023. Los datos mismos se pueden descargar de https://data.mendeley.com/datasets/bfrkzf5k64/1 ↩
-
Página web de Scikit-learn, en: https://scikit-learn.org/stable/auto_examples/linear_model/plot_ols.html y el libro Practical Statistics for Data Science. Bruce, Bruce, Gedeck, pg. 141. ↩
-
Practical Statistics for Data Science. Bruce, Bruce, Gedeck, pg. 150. y Python Data Science Handbook. Jake VanderPlas, pg. 419. ↩
-
La información sobre los diagramas de dispersión se encuentra en https://matplotlib.org/stable/gallery/mplot3d/scatter3d.html ↩
-
para generar un plano se sigue la información aquí https://www.tutorialspoint.com/how-to-plot-a-plane-using-some-mathematical-equation-in-matplotlib ↩
-
Python Data Science Handbook. Jake VanderPlas, pg. 422. ↩
-
La bibliografía para ésta sección es: Data Science for Public Policy. Chen, Rubin, Cornwall, pg. 165 ↩