Medición de Datos

Tipos de Variables

• contínua números reales en un rango. Ejemplo la estatura.
• discreta numeros enteros en un rango. Ejemplo la edad.
• Categórica Ordinal las observaciones toman etiquetas organizables.
• Categórica Nominal Las observaciones tienen etiquetas no organizables.

Implementación en Python

• Números Enteros Cómo 42. (En matemáticas son entero $\mathcal{Z}$)

  1 + 1
  5*8
  

  (python asume que son enteros)

• Números Flotantes Como 2.85 (En matemáticas son los racionales $\mathcal{Q}$)

  9/2
  

  Python entiende que estamos dividiendo flotantes. ¿cuál es el resultado?

• Texto En español: (Después hablaremos de la codificación, por ahora recuerde éstas letras: UTF-8.)

  'Estás en lo cierto'
  

• Lógica Se representan como True,False, 1 o 0.

• Error Operaciones no disponibles o incompatibles. #VALUE! o #¡VALOR!

• Las variables categóricas, tanto ordinal como nominal, se representancomo texto o variables lógicas.

Ejercicio

1. Clasifique los siguientes variables como número, texto o valor lógico.

a. 'palabra'

b. 3.5

c. 3,5

d. True

e. 1

f. 1/2

g. 'uno'

Conceptos Estadísticos

Video de ésta sección: https://youtu.be/45V4GQMG75c

• Universo: Conjunto de ‘Individuos’ Objeto de Investigación. Ejemplos:

  • Ríos en una vertiente
  • Habitantes de una zona.
  • Registros de datos de una entidad

• Observaciones: Cada uno de los valores de la variable que se registra para uno de los individuos. Se representa por: $\{X_1,X_2,...,X_N\}$

• Población: Conjunto de mediciones de una variable en cada ‘individuo’. Su tamaño es $N$. Ejemplos:

  • Caudal en punto medio. Longitud de los tramos navegables. Número de especies aprovechables
  • Último grado cursado. Lugar de vivienda. Edad.
  • Fecha y hora. Longitud en palabras. Tipo de solicitud.

• Muestra: Subconjunto representativo de la población. Sus características son similares a las de la población. Su tamaño es $n < N$.

• Parámetro: Característica de la población de referencia. Ej. promedio $\mu$, proporción $\pi$, total, varianza $\sigma^2$, distribucionalidad. Usualmente son desconocidos, obj. de investigación.

• Estadística (estadígrafo): Cálculos sobre los datos de la muestra, que estiman los parámetros de la población. Ej. promedio muestral $\overline X$, varianza muestral $S^2$, y proporción muestral $p$).

Medidas de tendencia central

https://youtu.be/45V4GQMG75c

• Promedio Aritmético
  • $\overline X = \frac{\sum_{i=1}^n X_i}{n}$ (sobre la muestra $n < N$ )
  • $\mu = \frac{\sum_{i=1}^N X_i}{N}$ (sobre la población )

• Mediana $\widetilde{X}$: Aprox. la mitad de las observaciones son mayores a la mediana.

  $\widetilde{X} = \begin{cases} X_{\left(\frac{n+1}{2}\right)} & \text{ n impar } \\ \frac{X_{\left(\frac{n}{2}\right)} + X_{\left(\frac{n}{2} + 1\right)}}{2} & \text{ n par } \\ \end{cases}$

• Moda: Es el dato que se repite más veces en una muestra.

Ejercicios

Un promedio sobre un conjunto pequeño de datos

Supongamos que tenemos la siguiente muestra de un conjunto de datos:

x = [1,5,1,1,1]

Vamos a hacer cálculos sobre ésta muestra, sin usar las funciones estadísticas del softare). Halle los valores de las medidas de tendencia central: moda, mediana, media.

Ahora un promedio sobre un conjunto más grande

Comencemos por generar un conjunto de datos.

import random as ran
ran.seed(8)
lista = [ran.choice([1,2,3,4,5,6]) for x in range(100)]

No es necesario que entendamos a profundidad ese código ahora. Pero le invito a que intente describir qué obtuvimos con éstas instrucciones antes de leer mi explicación.

.

.

.

OK, tenemos una lista de 100 números, donde los elementos son los números enteros del 1 al 6, elegidos al azar.

Ahora, usando Python, intentemos calcular las medidas de tendencia central.¹

Medidas de variabilidad

Videos de ésta sección en: https://youtu.be/TnChXWqAQN0

• Rango: valor máximo menos el valor mínimo

• Varianza

  • Varianza de la población:

    $\sigma^2 = \frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2$

  • Varianza de la muestra:

    $S^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \overline x)^2$

• Desviación estándar

  • Desviación estándar de la población

    $\sigma = \sqrt{\sigma^2}$

  • Desviación estándar de la muestra

    $S= \sqrt{S^2}$

  • Coeficiente de variación: Tamaño de la dispersión relacionada con el tamaño del promedio.

    $CV = \frac{S}{\overline X} \cdot 100$

Ejercicios

Sobre la muestra pequeña

Supongamos que tenemos la siguiente muestra de un conjunto de datos:

x = [1,5,1,1,1]

Vamos a hacer cálculos sobre ésta muestra, sin usar las funciones estadísticas del softare. Halle los valores de las medidas de variabilidad: Rango, Varianza, Desviación estándar.²

Sobre el conjunto más grande

Ahora tome de nuevo la lista que habíamos calculado anteriormente y calcule los estadísticos de variabilidad.³

Medidas de Localización

Percentiles Muestrales

Puede ver el libro de González páginas 124 a 133.

El percentil muestral $P_{\alpha}$ es un valor mayor o igual que al menos $\alpha$ por ciento de los datos y menor que al menos $100 − \alpha$ por ciento de los datos.

La posición del percentil $\alpha$, es: $\frac{\alpha}{100} (n+1)$. Los datos ordenados son:

$X : \{x_{1},x_{2},...,x_{n}\}$

El valor es una interpolación lineal entre los dos valores. Si la parte entera de la posición es $r$ y la fraccionaria es $f$, entonces va entre $x_r$ y $x_{r+1}$, así:

$P_{\alpha} = x_{r} + f\cdot(x_{r+1} - x_{r})$

Ejemplo, tiempos de espera

En una ventanilla de servicio al cliente se tienen los siguientes tiempos de espera en minutos:

12 19 13 3 7 3 3 3
7 7 4 6 10 9 21 12 3 10 3 4

Si los ordenamos tenemos:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
3 3 3 3 3 3 4 4 6 7 7 7 9 10 10 12 12 13 19 21

Calcule el $P_{90}$

Respuesta: primero necesitamos la posición y luego el valor:

• Posición: $\frac{90}{100} (21) = 18.9$, En este caso tenemos una parte entera de $r=18$ y una parte fraccionaria $f=0.9$

• Valor: $P_{90} = 13 + 0.9(19-13) = 18.4$

Medidas de forma y Simetría

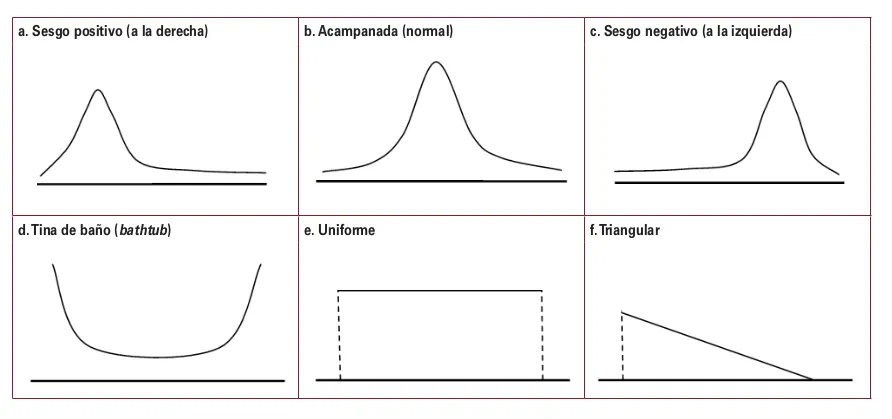
Coeficiente de Simetría

$g_1 = \frac{1}{n \cdot s^3} \sum_{i=1}^{n} \left(x_i - \overline{x}\right)^3$

• $g_1 > 0$: sesgo a la derecha
• $g_1 \approx 0$: distribución simétrica
• $g_1 < 0$: sesgo a la izquierda

En Excel

COEFICIENTE.ASIMETRIA

En LibreOffice

COEFICIENTE.ASIMETRIA.P

Ejemplo

De nuevo, trabajaremos con un conjunto grande de números que vamos a generar en Python. Llamémosle dist1:

import numpy as np
np.random.seed(22)
dist1 = np.array([np.random.poisson(2) for x in range(1000)])

En Python podemos calcular la asimetría con la función skew de la librería scipy.

import scipy.stats as stats
import statistics as st	
asimetria = stats.skew(dist1)

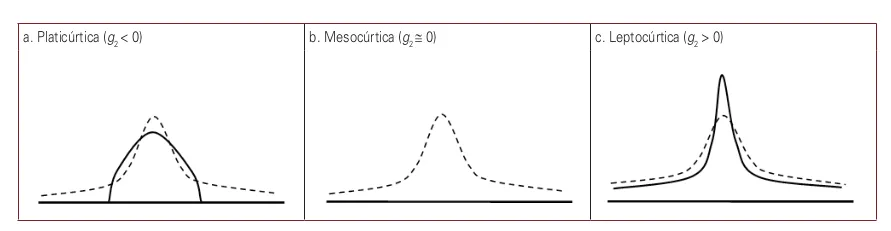
Curtosis

$g_2 = \frac{1}{n \cdot s^4} \sum_{i=1}^{n} \left(x_i - \overline{x}\right)^4 -3$

• $g_2 < 0$ menos apuntada que la distribución normal
• $g_2 \approx 0$ tan apuntada como la distribución normal
• $g_2 > 0$ más apuntada que la distribución normal

Solución ejercicios