Distribución de Frecuencia (Contento pg. 71)

Se usan para establecer cómo están agrupadas las observaciones de una variable, mediante la construcción de un conjunto de intervalos contiguos, no superpuestos, y la contabilidad del número de observaciones en cada uno de los intervalos (o su frecuencia).

Fórmula de Sturges (contento pg. 71)

El número de clases que se usan para $n$ datos está dado por:

$h = 1 + 3.322 \log_{10} n$

Para construir el diagrama:

Se calcula el número de clases (sturges), rango, ancho de clases.
Se definen los intervalos (clases)
Se cuenta el número de valores en cada clase

Esto lo hace el software, pero para entender cómo funciona hay que hacer un par de ejemplos “a mano”

extremo izquierdo	extremo derecho	marca de clase
[“cerca al” Minimo	ext.izq. $+$ ancho)	$ext. izq. + \frac{ancho}{2}$
[extr. der. anterior	ext.izq. $+$ ancho)	$ext. izq. + \frac{ancho}{2}$

Distribución de Frecuencia (\color{blue} Contento pg. 71)

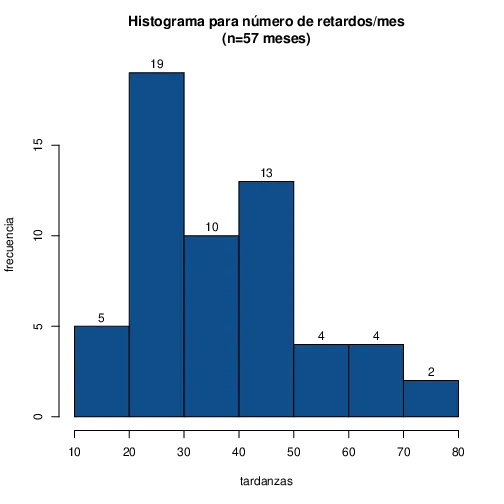
Ejemplo: Tardanzas

La tabla muestra las tardanzas a una empresa en 57 días:


68	63	42	27	30	36	28	32	79	27	22	23
24	25	44	65	43	25	74	51	36	42	28	31
28	25	45	12	57	51	12	32	49	38	42	27
31	50	38	21	16	24	69	47	23	22	43	27
49	28	23	19	46	30	43	49	12

Fórmula de Sturges (Contento pg. 71)

El número de clases que se usan para $n$ datos está dado por:

$h = 1 + 3.322 \log_{10} n$

como trabajar $n=57$ , luego:

h= 1 + 3.322 \log_{10} 57

La cuenta $1+3.322*log10(57)$ da como resultado 6.833, que se aproxima a 7.

Para construir el diagrama:

Número de clases (sturges): 7; máximo es 79, mínimo es 12, luego el rango es 67; ancho de clases: $67/7 = 9.57 \approx {\color{blue}10}$ (misma precisión de datos, aproximado hacia arriba)
Se definen los intervalos (clases)

extremo izquierdo	extremo derecho	marca de clase
“cerca al” Minimo	ext.izq. $+$ ancho	$ext. izq. + \frac{ancho}{2}$
$\color{red} [10$	${\color{red}10}+{\color{blue}10}={\color{deepgreen}20)}$	$10 + \frac{{\color{blue}10}}{2} = {\color{BrickRed}15}$
extr. der. anterior	ext.izq. $+$ ancho	$ext. izq. + \frac{ancho}{2}$
$\color{deepgreen}[20$	${\color{deepgreen}20}+{\color{blue}10}={\color{BlueViolet}30)}$	${\color{deepgreen}20} + \frac{{\color{blue}10}}{2} = {\color{BrickRed}25}$
extr. der. anterior	ext.izq. $+$ ancho	$ext. izq. + \frac{ancho}{2}$
$\color{BlueViolet}[30$	${\color{BlueViolet}30}+{\color{blue}10}={\color{Magenta}40)}$	${\color{BlueViolet}30} + \frac{{\color{blue}10}}{2} = {\color{BrickRed}25}$
…

Distribuciones de Frecuencia

Para construir el diagrama:

N. de clases: 7; máx. 79, mín. 12, rango 67; ancho $67/7 = 9.57 \approx {\color{blue}10}$
Se definen los intervalos (clases)

extremo izquierdo	extremo derecho	marca
$\color{red}[10$	${\color{red}20)}$	${\color{red}15}$
$\color{deepgreen}[20$	${\color{deepgreen}30)}$	${\color{deepgreen}25}$
$\color{BlueViolet}[30$	${\color{BlueViolet}40)}$	${\color{BlueViolet}25}$
$\color{Magenta}[40$	$\color{Magenta}50)$	$\color{Magenta}45$
$\color{Orchid}[50$	$\color{Orchid}60)$	$\color{Orchid}55$
$\color{MidnightBlue}[60$	$\color{MidnightBlue}70)$	$\color{MidnightBlue}65$
$\color{PineGreen}[70$	$\color{PineGreen}80)$	$\color{PineGreen}75$

Se cuenta el número de valores en cada clase

$\color{MidnightBlue}{68}$ , $\color{MidnightBlue}63$ $\color{Magenta}42$ $\color{deepgreen}27$ , $\color{BlueViolet}30$ , $\color{BlueViolet}36$ , 28, 32, 79, 27, 22, 23, 24, 25, 44, 65, 43, 25, 74, 51, 36, 42, 28, 31, 28, 25, 45, 12, 57, 51, 12, 32, 49, 38, 42, 27, 31, 50, 38, 21, 16, 24, 69, 47, 23, 22, 43, 27, 49, 28, 23, 19, 46, 30, 43, 49, 12)

Esto lo hace el software, pero para entender cómo funciona hay que hacer un par de ejemplos “a mano”

Ejercicio / Tarea

Termine de clasificar todos los valores y construya el histograma

Histogramas (González, pg 46 - 51)

En Excel, datos en una columna. Insertar ➡️ Histograma


68	63	42	27	30	36	28	32	79	27	22	23
24	25	44	65	43	25	74	51	36	42	28	31
28	25	45	12	57	51	12	32	49	38	42	27
31	50	38	21	16	24	69	47	23	22	43	27
49	28	23	19	46	30	43	49	12


68	63	42	27	30	36	28	32	79	27	22	23
24	25	44	65	43	25	74	51	36	42	28	31
28	25	45	12	57	51	12	32	49	38	42	27
31	50	38	21	16	24	69	47	23	22	43	27
49	28	23	19	46	30	43	49	12

1. Distribuciones de frecuencias

Distribución de Frecuencia (Contento pg. 71)

Fórmula de Sturges (contento pg. 71)

Para construir el diagrama:

Distribución de Frecuencia (\color{blue} Contento pg. 71)

Ejemplo: Tardanzas

Fórmula de Sturges (Contento pg. 71)

Para construir el diagrama:

Distribuciones de Frecuencia

Para construir el diagrama:

Ejercicio / Tarea

Histogramas (González, pg 46 - 51)


68	63	42	27	30	36	28	32	79	27	22	23
24	25	44	65	43	25	74	51	36	42	28	31
28	25	45	12	57	51	12	32	49	38	42	27
31	50	38	21	16	24	69	47	23	22	43	27
49	28	23	19	46	30	43	49	12