Análisis de varianza

• Se busca comparar tres o más grupos (ej. 4 medicamentos, 4 dosis, etc)
• ¿cómo comparar promedios, si hay dispersión entre los grupos? efecto de la varianza:
• varianza dentro del grupo, vs. varianza entre los grupos.

Elementos del diseño de experimento

Experimento: situación planeada y controlada. Prueba o serie de pruebas para identificar causas

• Unidades Experimentales: objetos a medir (ej. pacientes, registros públicos, etc)
• ${\color{green} Respuesta}$: Variable dependiente a ser analizada.
• ${\color{blue} Factores}$: Variables independientes que afectan la respuesta.
• ${\color{red} Nivel}$: Grado de intensidad de un factor
• ${\color{applegreen} Tratamiento}$: Combinación de factores a diferentes niveles

Ejemplo:

Tomemos la siguiente situación problemática. Estudiar el crecimiento de una planta, en función de tres variedades de fertilizante y de cuatro tipos de suelo.

• Unidades Experimentales Planta
• ${\color{green} Respuesta}$ Longitud de Crecimiento
• ${\color{blue} Factores}$ A: fertilizante, B:Suelo
• ${\color{red} Nivel}$ tres para A: A1,A2,A3;cuatro para B: B1,B2,B3,B4
• ${\color{applegreen} Tratamiento}$ Combinaciones de A y B

ANOVA a una vía

Un factor, $k$ niveles, buscamos comparar los promedios de una variable en los $k$ grupos. Se seleccionan muestras aleatorias independientes de las $k$ poblaciones (diseño completamente aleatorizado).

Supuestos

• La variable dependiente se distribuye normal en cada grupo
• La varianza es igual entre poblaciones
• Las Observaciones son independientes.

Hipótesis

• $H_0: \mu_1 = \mu_2 = ... = \mu_k$ los grupos tienen el mismo promedio (no hay efecto del tratamiento)
• $H_a:\exists i / \mu_i \neq \mu_j \forall j = 1,2,...,k$ un $\mu_k$ produce efecto diferente.

Ejemplo 0: Dados

Tenemos 12 dados de 6 caras y 6 dados de 4 caras. Si hacemos 3 grupos de la siguiente forma:

Si lanzamos los dados y generamos una tabla, ¿esperamos una diferencia en el promedio entre grupos?

Si los 3 grupos son:

Si lanzamos los dados y generamos una tabla, ¿esperamos una diferencia en el promedio entre grupos?

¿Hay más diferencia entre promedios de los grupos rojos (1,2,3) o entre los grupos azules (4,5,6)?

Hipótesis

• $H_0: \mu_1 = \mu_2 = ... = \mu_k$ los grupos tienen el mismo promedio (no hay efecto del tratamiento)
• $H_a:\exists i / \mu_i \neq \mu_j \forall j = 1,2,...,k$ un $\mu_k$ produce efecto diferente.

$y_{ij}$, la $j$-ésima observación del $\color{blue}i-ésimo\ tratamiento$

$y_{{\color{blue}i}\square} = \sum_{j=1}^n y_{{\color{blue}i}j}$ : es la suma del ${\color{blue}i-ésimo\ grupo}$

$\overline{y_{{\color{blue}i}\square}} = \frac{y_{{\color{blue}i}\square}}{n}$ es el promedio del ${\color{blue}i-ésimo grupo}$

${y_{\square\square}} \sum_{j=1}^n\sum_{i=1}^k y_{{\color{blue}i}j}$ es la suma de todos los grupos

$\overline{y_{\square \square}} = \frac{y_{ \square \square}}{kn}$ es el promedio de todos los datos

Modelo

$y_{ij} = \mu_i + \epsilon_{ij} \ i=1,2,...,k \ j=1,2,...,n$

Suma de Cuadrados Total ${\color{red}SST}$

O variación total en el experimento: ${\color{red}SST}= \sum_{i=1}^k\sum_{j=1}^n (y_{ij}-\overline{y_{\square\square}})^2$

$y_{ij} - \overline{y_{\square\square}}$ es la distancia de cada medición al promedio. Luego la ${\color{red}SST}$ es la suma de los cuadrados de las distancias al promedio.

Ejemplo 1

Si tenemos Los siguientes grupos:

Para hallar la suma de cuadrados total calculamos total y media por grupo:

Y calculamos la suma de todos los datos y su promedio:

${y_{\square\square}} = 182$
$\overline{y_{\square \square}} = 12.13$

Ejemplo 2 (KA), SST

De Khan Academy, en el enlace: https://youtu.be/tH01ocwZGkQ?si=C7f4ZRoxIGunajC8

Suma de cuadrados entre tratamientos y dentro de tratamientos

La expresión para SST se puede modificar haciendo algo de álgebra (como lo muestra el profesor Contento en su libro del año 2019). Después de ésto se llega a :

${\color{red}SST} = {\color{blue}SCTr} + {\color{green}SSE}$

${\color{red}SST} = {\color{red}\sum_{i=1}^k\sum_{j=1}^n (y_{ij}-\overline{y_{\square\square}})^2} = {\color{blue}\sum_{i=1}^k\sum_{j=1}^n (\overline{y_{i\square}}-\overline{y_{\square\square}})^2} + {\color{green}\sum_{i=1}^k\sum_{j=1}^n (y_{ij}-\overline{y_{i\square}})^2}$

Donde: ${\color{red}SST}$ es la suma de cuadrados total que ya conocemos, y

• ${\color{blue}SCTr}$ que se define como $\sum_{i=1}^k\sum_{j=1}^n (\overline{y_{i\square}}-\overline{y_{\square\square}})^2$ es la variabilidad debida a diferentes tratamientos, suma de cuadrados entre tratamientos.

• ${\color{green}SSE}$ que se define como $\sum_{i=1}^k\sum_{j=1}^n (y_{ij}-\overline{y_{i\square}})^2$ es la variación de los sujetos que pertenecen a un tratamiento, es decir la suma de cuadrados dentro de tratamientos. LLamado también Error.

Volviendo al…

Ejemplo 1

Tenemos que:

${\color{red}SST} = (8-12.13)^2 + (7-12.13)^2 + ... + (15-12.13)^2 + (12-12.13)^2$

${\color{blue}SCTr} = (9.4 - 12.13)^2 +(9.4-12.13)^2 + ... + (13-12.13)^2 + (13-12.13)^2$

${\color{green}SSE} = (8-9.4)^2 +(7-9.4)^2 + ... + (15-13)^2+(12-13)^2$

Ejemplo 2

Para calcular SCTr y SSE para el ejemplo 2, siga el enlace: https://www.youtube.com/watch?v=l_VHVIF7_cs

Grados de Libertad

Recordemos que estamos interesados en identificar si existe variabilidad entre diferentes grupos. Ahora, como necesariamente habrá más variabilidad si hay más grupos y más datos, es necesario tener en cuenta los grados de libertad.

• Grados de libertad de los tratamientos: ${\color{blue}gl(Tr) = k -1}$, será el número de tratamientos menos uno.

• Grados de libertad entre tratamientos: ${\color{red}gl(T) = kn -1}$ será el número total de datos menos uno.

• Grados de libertad dentro de los tratamientos: ${\color{green}gl(E)} = {\color{red}gl(T)} - {\color{blue}gl(Tr)} = \\kn-1 -k +1 = {\color{green}k(n-1)}$ es la resta de los dos anteriores.

Cuadrados medios

Con los grados de libertad se calculan los cuadrados medios de variación

• $CMTr = \frac{{\color{blue}SCTr}}{gl(Tr)} = \frac{{\color{blue}SCTr}}{k-1}$, son los cuadrados medios ${\color{blue}entre}$ tratamientos

• $CME = \frac{{\color{green}SSE}}{gl(E)} = \frac{{\color{green}SSE}}{k(n-1)}$ son los cuadrados medios ${\color{green}dentro}$ de los tratamientos.

Prueba de Hipótesis

Si el tratamiento no funciona, los promedios serán todos iguales. Si el tratamiento funciona habrá uno de ellos que es diferente. Entonces podemos lanzar las hipótesis:

• $H_0: \mu_1 = \mu_2 = ... = \mu_k$
  Entonces $\overline{y_{1\square}} \approx \overline{y_{2\square}} \approx ... \approx \overline{y_{k\square}}$ {La variación entre grupos ${\color{blue}(CMTr)}$ es similar a la variación dentro de grupos ${\color{green}(CME)}$.

• $H_a:\exists i / \mu_i \neq \mu_j \forall j = 1,2,...,k$, es decir, hay un promedio diferente. Hay un $\overline{y_L}$ que $\overline{y_L} \neq \overline{y_1} \approx ... \approx \overline{y_k}$} Hay más variación al comparar los grupos ${\color{blue}(CMTr)}$ que la variación dentro de los grupos ${\color{green}(CME)}$.

Ejercicios

Aquí se pueden hacer los ejercicios 1 y 2 de Contento, página 372

Ejemplo

Supongamos que para un proceso tenemos los siguientes valores y sus respectivos promedios.

Los representamos en la siguiente gráfica.

Aquí podemos ver que los poromedios tienden a estar cerca entre ellos.

Ahora, $\mu \approx -0.0416$. Entonces $SCTr = 3 \cdot (-0.25-0.0416)^2 + 3 \cdot (0 - 0.0416) ^2 + 3 \cdot (-0.125-0.125)^2 = 0.28125$ y ${\color{blue} CMTR=0.09375}$ $SSE = (-3+0.25)^2 +(-1.2+0.125)^2 + ... + (3-0.125)^2 \approx 38.2818$ y ${\color{green}CME \approx 4.253}$. Fijate que no se cumple que ${\color{blue}(CMTr)}$>${\color{green}(CME)}$

Ahora si la tabla fuese diferente, por ejemplo la siguiente:

Aquí los valores azules están alejados de los verdes y rojos, como se puede ver en la gráfica:

Calculamos los valores, encontrando

$\mu \approx 0.73$

$SCTr \approx 53.41$

${\color{blue} CMTr \approx 26.703,}$

$SSE \approx 4.22$,

${\color{green}CME \approx 0.489}$

Vemos que se cumple que ${\color{blue}(CMTr)}$>${\color{green}(CME)}$

Prueba de Hipótesis para ANOVA

Los cuadrados medios $CMTr = \frac{{\color{blue}SCTr}}{k-1}$ y $CME = \frac{{\color{green}SSE}}{k(n-1)}$ representan variables ${\color{blue}entre}$ grupos y ${\color{green}dentro}$ de los grupos. Su división $f_c=\frac{{\color{blue}CMTr}}{{\color{green}CME}}$ es una variable aleatoria que se distribuye como una función $F$ con $k-1$ y $k(n-1)$ grados de libertad.

• $f_c=\frac{{\color{blue}CMTr}}{{\color{green}CME}}$

• Si la $H_0$ es verdadera (no hay efecto del tratamiento, $H_0: \mu_1 = \mu_2 = ... = \mu_k$), CMTr (y por lo tanto $f_c$) es pequeño.

• Si $f_c$ es alto hay evidencia de que $H_0$ es falsa. (${\color{blue}variabilidad\ \textbf{entre}}$ tratamientos mayor que ${\color{green} \textbf{dentro de}\ tratamientos}$). Por lo menos un promedio es diferente y se rechaza $H_0$

• La probabilidad de que aleatoriamente, sólo por coincidencia, ocurra éste evento se calcula como: $P(F_{(k-1),k(n-1)}>f_c)$. A medida que este valor se hace más pequeño es cada vez menos probable.

• La prueba indica “nivel de significancia” $\alpha$, que es una medida de qué tan improbable es el resultado. Usualmente se trabaja con un nivel de significancia del 5%, es decri 0.05. Cuando la probabilidad es menor a éste valor se concluye que no se debió al azar.

Ejemplo (Contento 2019, pg. 362)

Niveles de atención (minutos) de lectura matutina, en tres grupos

Para trabajarlo en Python:

• Se cargan las librerías

import pandas as pd
import statsmodels.api as sm
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.stats as stats
plt.ion()
from statsmodels.formula.api import ols

• Se ingresan los datos

datos = pd.DataFrame({'atencion':[8,7,9,13,10,14,16,12,17,11,10,12,16,15,12],'tipo_desayuno':['sin','sin','sin','sin','sin','ligero','ligero','ligero','ligero','ligero','completo','completo','completo','completo','completo']})

• Se crea un modelo explicativo, en este caso lineal:

lm = ols('atencion ~ C(tipo_desayuno)',data=datos).fit()

• Se construye el ajuste por ANOVA:

tabla_anova = sm.stats.anova_lm(lm,typ=2)
tabla_anova

El resultado es el siguiente:

La tabla indica los valores de la suma de cuadrados, los grados de libertad de grupos y datos, el valor de $F$ y la probabilidad de encontrar ese valor por azar, $0.027326$. Como este valor es más pequeño al 5%, pero más grande al 1%, se concluye el resultado es significativo a un nivel de 5%.

Ejemplo 2, Khan Academy:

Se puede ver en el siguiente video: https://youtu.be/46CVRPdlKHc?si=0xxT_TOcSO5rWHV0

Condiciones para ANOVA

Para que se pueda aplicar el método del análisis de varianza, y sus resultados tengan sentido, se tinen que cumplir una serie de condiciones.

1. Normalidad de los residuales: la distribución de los errores experimentales debe ser una distribución gaussiana.

2. Homogeneidad de la varianza (homocedasticidad): las varianzas de las variables dependientes deben ser aproximadamente similares entre los grupos de tratamiento.

3. Independencia: no hay relación entre las observaciones de diferentes grupos, son independientes entre ellos

Y relacionado con estos tenemos también la continuidad de la variable dependiente, ya que cuando esta variable no lo és se invalida la condicion de normalidad y homogeneidad de la varianza.

Pruebas para las condiciones

Se investigan con estadísticos de prueba (Shapiro, Levene, entre otros) o gráficamente (gráficos de residuos QQ o histogramas)

Normalidad

Shapiro

Usando el test de shapiro:

stats.shapiro(lm.resid)

El resultado son dos números, la estadística de prueba y el nivel de significacncia, $\alpha$. La hipótesis nula es que si se distribuyen de manera normal. En este caso se obtiene el siguiente texto: ShapiroResult(statistic=np.float64(0.9272863300806745), pvalue=np.float64(0.24845535561613769)). Es decir, el valor del estadístico de prueba es 0.9272863300806745, y la significancia es 0.24845535561613769. Cómo éste valor no es menor a 0.05, no tenemos evidencia contra la hipótesis nula; es decir que aceptamos que se cumple la condición de normalidad de los rediduos.

Gráficamente

fig = plt.figure(figsize= (10, 10))
ax = fig.add_subplot(111)

normality_plot, stat = stats.probplot(lm.resid, plot= plt, rvalue= True)
ax.set_title("Probability plot of model residual's", fontsize= 20)
ax.set

Se obtiene la siguiente gráfica:

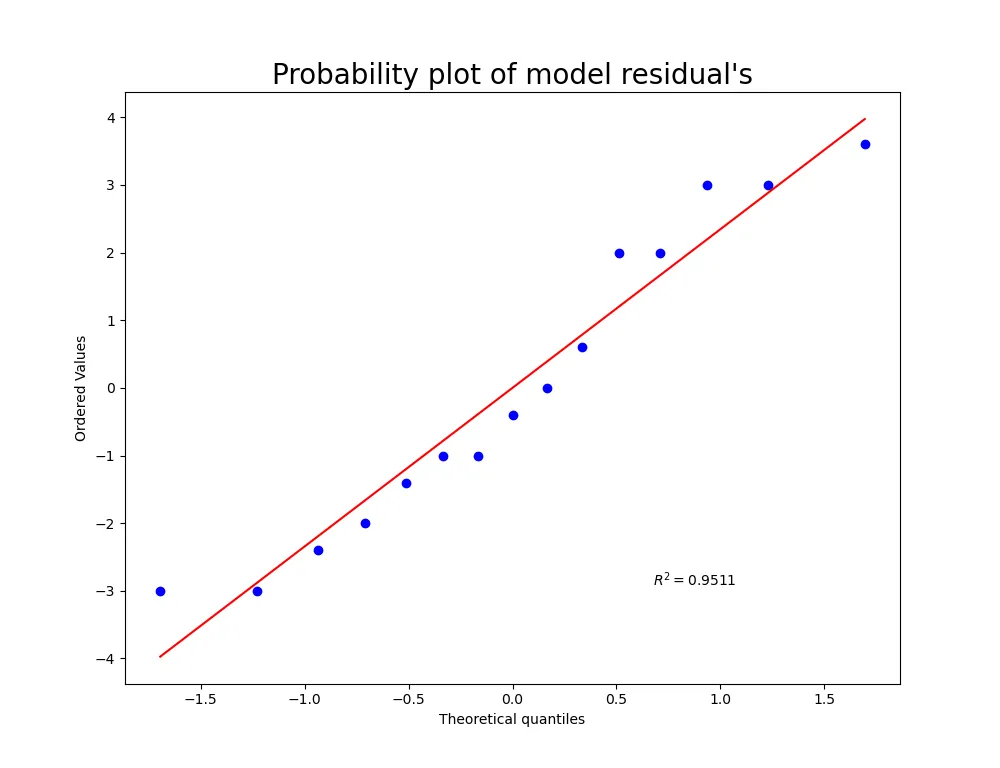
Homogeneidad de la varianza

Primero construimos una tabla de los datos divididos por categorías.

data = [datos['atencion'][datos['tipo_desayuno'] == 'sin'],
        datos['atencion'][datos['tipo_desayuno'] == 'ligero'],
        datos['atencion'][datos['tipo_desayuno'] == 'completo']]

A continuación se genera la gráfica.

fig = plt.figure(figsize= (10, 10))
ax = fig.add_subplot(111)

ax.set_title("Tiempos de atención", fontsize= 20)
ax.set


ax.boxplot(data,
           labels= ['sin', 'ligero', 'completo'],
           showmeans= True)

plt.xlabel("Desayuno")
plt.ylabel("Atención")

El resultado es la siguiente gráfica:

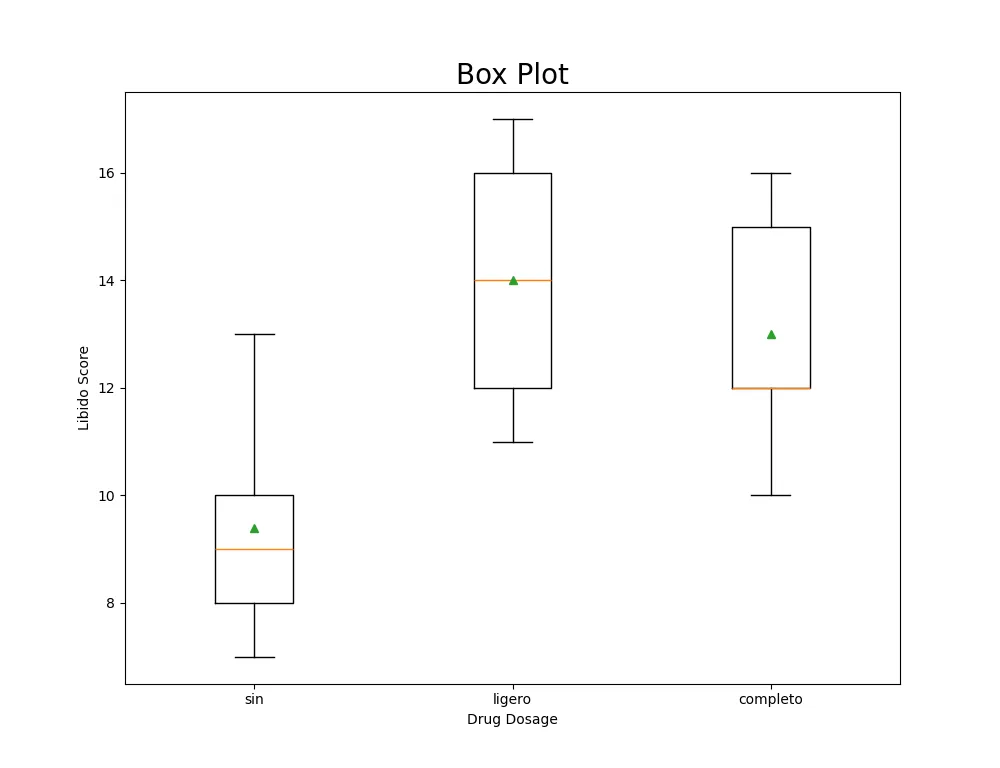
En el cuadrado verde está el promedio . La línea naranja es la mediana.

¿usted diría que la distribución es simétrica?

Bibliografía

• https://www.reneshbedre.com/blog/anova.html
• https://www.pythonfordatascience.org/anova-python/