Hipótesis

Proposiciones acerca de las características de una variable o acerca de la relación entre dos o más variables.

H. : La edad promedio a la que comienza el consumo de cigarrillo en Colombia es de 15 años
El cociente intelectual de la población sigue una distribución normal
El cancer de pulmón es más frencuente entre fumadores que no fumadores.
El nivel de estrés de una person a se relaciona con el número de horas que trabaja

Características

Se refieren a una situación real
Se relacionan con variables concretas, precisas, comprendibles
Las variables se relacionan de forma clara y lógica
Se relacionan a variables cuantificables y medibles
Se pueden probar o desprobar.

Prueba de Hipótesis

La $H_a$ alternativa: es nuestra expetativa. Si tenemos un valor umbral, $\theta_0$ , la hipótesis alternativa puede ser:
1. $\theta<\theta_0$ , la hipótesis es que el valor del parámetro es menor que el valor umbral.
2. $\theta=\theta_0$ , la hipótesis es que el valor del parámetro es igaul al valor umbral
3. $\theta>\theta_0$ , la hipótesis es que el valor del parámetro es mayor al valor umbral
La hipótesis nula $H_0$ , hipótesis de no efecto, hipótesis de no diferencia.
1. Por ejemplo, si la hipótesis nula es $\theta<\theta_0$ , entonces la hipótesis alternativa es que el valor del parámetro $\theta$ es mayor al umbral $\theta_0$ , es decir es: $H_a: \theta>\theta_0$
2. Si la hipótesis nula es $\theta=\theta_0$ , entonces la hipótesis alternativa es que $\theta \neq \theta_0$ , es decir es: $H_a: \theta \neq \theta_0$
3. Si la hipótesis nula es $\theta > \theta_0$ , entonces la hipótesis alternativa es que el valor del parámetro $\theta$ es menor al umbral $\theta_0$ , es decir es: $H_a: \theta < \theta_0$
Región de rechazo: Si no se cumple $H_0$ , la dist. de muestreo dará un valor extremo. Es decir, es poco probable que $\theta$ caiga en ese valor. $\alpha$ define un rango donde desestimamos $H_0$ , por improbable.

(como creemos que pasará $H_a$ , esperamos que no pase $H_0$ , luego la estadística de muestreo lleva a rechazo)
Estadística de prueba: distribución de muestreo, dado que $H_0$ es cierto. Muestra como se espera que se comporten los datos muestrales si la hipótesis nula fuese cierta.

Ejemplo (Hipótesis)

Un mandatario local dice que durante su mandato por lo menos el 5% de los viajes en la ciudad se harán en bicicleta. Si falla, menos del 5% de los viajes en la ciudad se harán en bicicleta. Se plantea la variable: X: fracción de los viajes que se realizan en bicicleta.

En una investigación se tiene indicios de que no se cumplió la meta (por ejemplo los colectivos ciclistas tienen esa impresión). Plantea la hipótesis: $H_a$ la fracción de los viajes es menor a 0.05.

La hipótesis nula: $H_0$ la fracción de los viajes es mayor a 0.05.

No tenemos toda la información de la realidad, pero sabemos que si el 5% de los viajes son en bicicleta, y si tomamos una muestra suficientemente grande de los viajes muy probablemente encontremos suficientes viajes en Bicicleta.

Prueba de Hipótesis para el promedio, $\mu$

Como primer caso, piense que la hipotesís nula es que el promedio es igual o mayor a un valor umbral: $H_0: \mu \geq \mu_0$

En este caso la hipótesis alteranativa es: el parámetro real es menor a ese umbral, es decir que $H_a: \mu < \mu_0$

Valor crítico para región de rechazo

El valor crítico es el valor de la distribución t de student, con parámetros $\alpha$ y $n-1$ grados de libertad. Se simboliza como: $t_{\alpha;n-1}$ . En la gráfica es la región azul:

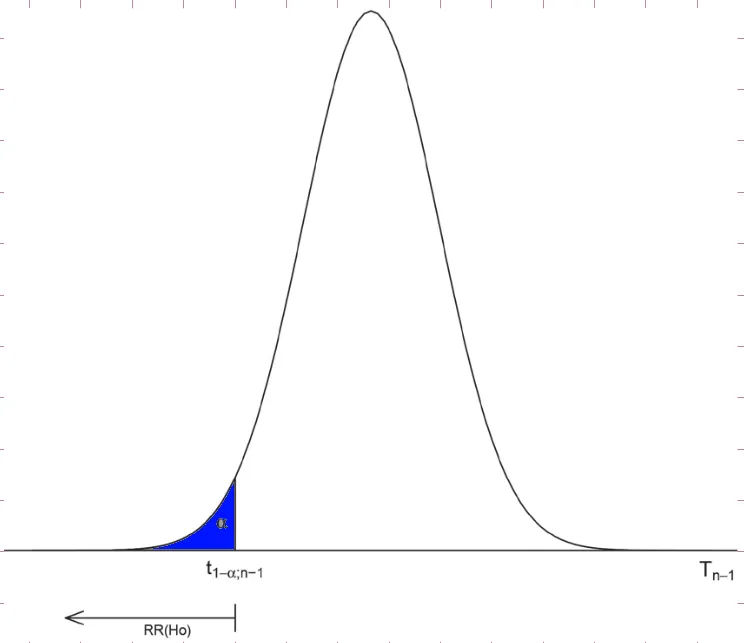$región de rechazo H_a:\mu < \mu_0, H_0:\mu \geq \mu_0$ $H_a:\mu < \mu_0$ , $H_0:\mu \geq \mu_0$

Para calcularlo en Python se usa el siguiente código:

from scipy.stats import t
t.ppf(alfa,10)

Atención En el software R se usa $1-\alpha$ .

Estadística de prueba.

La estadística de prueba es una distribución t-student con $n-1$ grados de lib. $t_c=\frac{\overline{x}-\mu_0}{s/\sqrt{n}}$

Ejemplo, valor del parámetro “promedio” en una prueba médica

Una empresa dice que la potencia de la medicina es del 80%, pero al revisar 100 cápsulas el valor promedio calculado es de 79.7% con una desviación estándar de $s=0.8\%$ . ¿hay suficiente evidencia para refutar a la empresa?

Datos

Primero organicemos los datos del enunciado en una tabla.

característica	valor
Variable	X: potencia
tamaño de la muestra	n=100
promedio	$\overline{x}=79.7$
desviación estándar	$s=0.8$
confianza	$\alpha=0.05$

El valor de confianza se toma en 0.05 por defecto (a menos que se nos informe algo diferente)

Hipótesis

En este caso tenemos

Hipótesis Nula $H_0:\mu=80 \%$ . Se acepta lo que dice la empresa
Hipótesis alternativa $H_a:\mu<80 \%$ . No se acepta, porque tenemos evidencia de lo contrario, ya que medimos la concentración promedio en 79.7%, que es menor al 80%.

Región de Rechazo

Sabemos que el promedio una muestra aleatoria no necesariamente tendrá 80% de potencia. Ahora, si un valor de promedio es muy pequeño, podemos decir que la empresa no cumple. ¿que tan bajo es bajo? Si cae en la región de rechazo.

Para calcular la región de rechazo necesitamos el valor crítico para defenir la región de rechazo. Se trata de $t_{1-\alpha,n-1}$ , en este caso $t_{0.95,99}$

En Python:

from scipy.stats import t
t.ppf(0.95,99)
-1.6603911559963902

Quiere decir que valores el estadístico de prueba a la izquierda de -1.6604 son poco probables, entonces se rechaza la hipótesis nula. En este caso quiere decir que hay evidencia de que la empresa no cumple.

Estadístico de prueba

Es:

$t=\frac{79.7-80}{0.8/\sqrt{100}} -3.75$

Como tenemos que $t \leq t_c$ , entonces rechazamos la hipótesis nula.

Tipos de prueba de hipótesis para el promedio

Cuando la hipótesis nula es $\mu \geq \mu_0$ (promedio mayor o igual a un valor)

$H_0: \mu \geq \mu_0$
$H_a$ : $\mu<\mu_0$
Región de rechazo: $\alpha \approx 0.05$
Estad. de prb.: T-Student: $t_c=\frac{\overline{x}-\mu_0}{s/\sqrt{n}}$
Rechazo: $t_c < t_{\alpha;n-1}$
Python: t.ppf(alfa,n-1)
R: qt(1-alfa,n-1,lower.tail=F)

$región de rechazo H_a:\mu < \mu_0, H_0:\mu \geq \mu_0$

Cuando la hipótesis nula es $\mu \neq \mu_0$ (promedio mayor o igual a un valor)

$H_0: \mu=\mu_0$
$H_a$ : $\mu \neq \mu_0$
Región de rechazo: $\alpha \approx 0.05$
$t_c=\frac{\overline{x}-\mu_0}{s/\sqrt{n}}$
Rechazo:
- $t_c < t_{\alpha/2;n-1}$
- Python: t.ppf(alfa/2,n-1)
- $t_c > t_{1-\alpha/2;n-1}$
- Python: t.ppf(1-alfa/2,n-1)

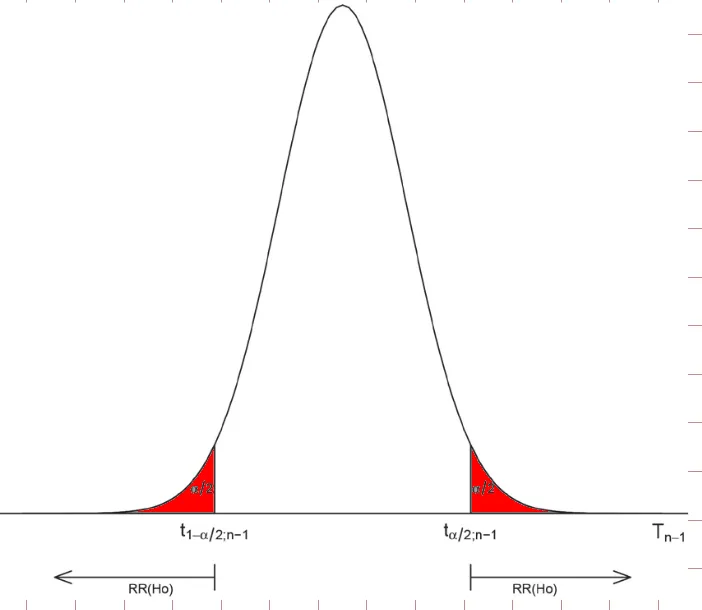
$región de rechazo H_a:\mu \neq \mu_0, H_0:\mu = \mu_0$

Cuando la hipótesis nula es $\mu \neq \mu_0$ (promedio mayor o igual a un valor)

$H_0: \mu \leq \mu_0$
$H_a$ : $\mu>\mu_0$
Región de rechazo: $\alpha \approx 0.05$
$t_c = \frac{\overline{x}-\mu_0}{s/\sqrt{n}}$
Rech.: $t_c>t_{1 - \alpha;n-1}$ $t_{c} > t_{1 - α; n - 1}$
- Python: t.ppf(1-alfa,n-1)

$región de rechazo H_a:\mu > \mu_0, H_0:\mu \leq \mu_0$

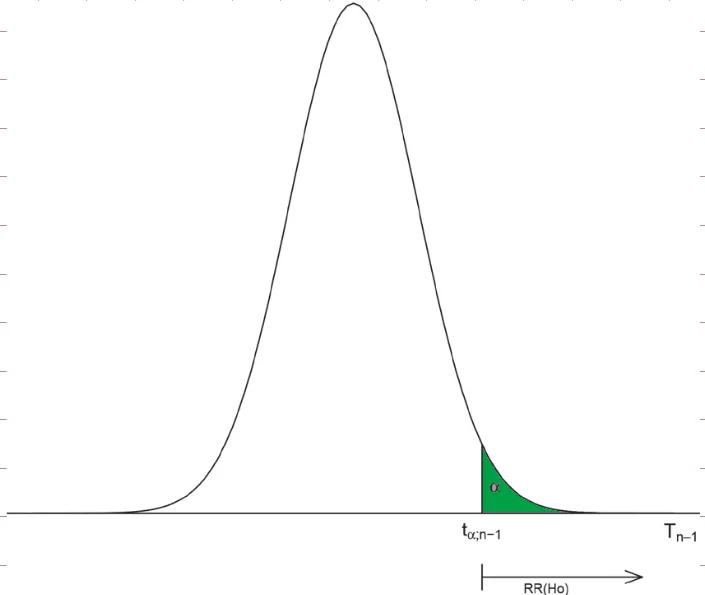
Recursos

Hipótesis https://youtu.be/F5iJBN50mms?si=Qd-wCfM0rvz5XgkE
Prueba de Hipótesis https://youtu.be/Tt8PIJY-2Pk?si=RoOQ5q1-IBjW6NAV
Prueba de Hipótesis para el promedio https://youtu.be/764-6M9JPtY?si=I-FCU52Hpl61dJbj
Prueba de Hipótesis promedio y proporción https://youtu.be/NJioD-owWZU?si=g7mtzlONKCOYIpom
Tests en python
- https://www.statology.org/how-to-find-the-t-critical-value-in-python/
- https://www.askpython.com/python/examples/find-critical-value
Contento, capítulo 5

Prueba de Hipótesis

Hipótesis

Características

Prueba de Hipótesis

Ejemplo (Hipótesis)

Prueba de Hipótesis para el promedio, μ\muμ

Valor crítico para región de rechazo

Estadística de prueba.

Ejemplo, valor del parámetro “promedio” en una prueba médica

Datos

Hipótesis

Región de Rechazo

Estadístico de prueba

Tipos de prueba de hipótesis para el promedio

Cuando la hipótesis nula es μ≥μ0\mu \geq \mu_0μ≥μ0​ (promedio mayor o igual a un valor)

Cuando la hipótesis nula es μ≠μ0\mu \neq \mu_0μ=μ0​ (promedio mayor o igual a un valor)

Cuando la hipótesis nula es μ≠μ0\mu \neq \mu_0μ=μ0​ (promedio mayor o igual a un valor)

Recursos

Prueba de Hipótesis para el promedio, $\mu$

Cuando la hipótesis nula es $\mu \geq \mu_0$ (promedio mayor o igual a un valor)

Cuando la hipótesis nula es $\mu \neq \mu_0$ (promedio mayor o igual a un valor)

Cuando la hipótesis nula es $\mu \neq \mu_0$ (promedio mayor o igual a un valor)