Distribución de Muestreo del Promedio

En clase del 14 de marzo leímos del libro de contento, páginas 237 a la 243.

Parámetro

Caracteristica de una población. Ejemplos:

• Rango de la variable “número de solicitudes semanales a la alcaldía”
• Distancia promedio recorrida por las personas en sus desplazamientos en el municipio.
• Asimetría de la distribución de desechos aprovechables generados en una zona.

Estadística

Estimación del parámetro al calcular en una muestra.

Con los mismos ejemplos:

• Para estimar el rango de la variable “número de solicitudes semanales a la alcaldía”, se registran las solicitudes durante un mes, es decir 4 datos, y se calcula el rango entre esos datos.
• Para estimar la distancia promedio recorrida por las personas en sus desplazamientos en el municipio, se hace una encuesta de movilidad en la que se toma el dato del desplazamiento de un grupo de personas, no de todas.
• Para estimar la asimetría de la distribución de desechos aprovechables generados en una zona, se toman valores de la cantidad de desechos aprovechables generados durante varios días, y se construye un histograma. Luego se calcula su asimetría.

En estos casos se hace un cálculo sobre los valores de la muestra, que llamamos estadística, con el objetivo de estimar el valor del parámetro.

Distribución de Muestreo

Para una variable aleatoria $X$, se puede tomar una muestra de tamaño $n$ y calcular una estadística sobre la muestra (como $\overline{x}_1$)

Si se hubiera tomado otra muestra $2$, se tendría otro $\overline{x}_2$

El conjunto de los $\{\overline{x}\}$ es la distribución de muestreo del promedio.

Ejemplo

Supongamos que el universo es un conjunto de discos. La variable que nos interesa es el radio. Queremos estimar el valor del promedio del radio. Si son muchos discos, no podemos hacer un censo. Como ejemplo, pensemos en los siguientes discos:

Podemos tomar una muestra, mostrada aquí con rojo, y calcular el radio promedio. Obtenemos $\overline{r}=0.41$:

U otra muestra, mostrada aquí con verde, obteniendo $\overline{r}=0.3625$

Ninguno de estos promedios es el promedio “real”, pero creemos que están cerca a ese valor. Entonces hacemos un análisis estadístico, en el que la variable es el radio promedio.

¿cómo se distribuye la variable aleatoria $X: \overline{r}$?

Distribución de Muestreo

Teorema del límite central (TLC)

El TLC nos garantiza la relación entre los estadísticos y el parámetro.

Sea $X$ una varible aleatoria. Su valor esperado (promedio) es: $E(X) = \mu$ , su varianza es $V(X) = \sigma^2$.

• De una muestra aleatoria: $X_1 = \{X_{11},X_{12},...,X_{1n}$}, se calcula un promedio, llamémoslo $\overline{X_1}$.
• De otra muestra $X_2$, otro promedio, llamémoslo $\overline{X_2}$.
• Y así sucesivamente para una muestra 3, 4, etc.

El TLC garantiza que la distribución de los promedios $\overline{X}$ tiende a una distribución normal cuando crece $n$: $\overline{X_n} \approx N(\mu,\sigma/\sqrt{n})$, cuando $n \to \infty$.

¿esto que nos dice?

Suponga que tiene una distribución desconocida. Lo que garantiza el TLC es que al hacer una distribución de los promedios muestrales usted tiene una estimación del promedio de esa distribución desconocida, y la desviación estándar de esa distribución desconocida.

Ejemplo

Supongamos que tenemos una variable aleatoria que queremos caracterizar. Ahora, esa variable puede distribuirse de manera uniforme, pero supongamos que eso no lo sabemos.

Por ejemplo, usted encuentra un problema real, decide usar estadística para caracterizarlo. Define una variable. Pero no sabe si la variable que definió es uniforme o no. ¿cómo encuentra el promedio?

Específicamente, digamos que $X$ es una variable aleatoria uniforme en $(0,10)$. Representamos la variable por el siguiente histograma.

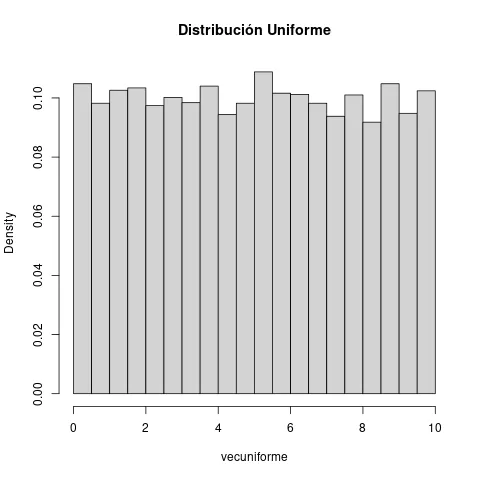
Si quisieramos saber el promedio de la variable $X$, podríamos hacer un censo del valor de la variable y promediar. Si esto es impráctico, podemos tomar una muestra y calcularle el promedio. Pero para tener un valor más cercano al promedio poblacional, podemos hacer esto varias veces, tomar varias muestras y calcular el promedio sobre cada muestra. Nos hacemos la siguiente pregunta:

¿Cómo se distribuye la variable promedios de $\overline{X}$?

Tomamos una primera muestra, y obtenemos los valores: 0.6564121 4.7021593 4.9894877 3.3917462 1.7230563 9.4006784 4.6939857 2.3625959 7.1384810 7.2330379.

Al calcular el promedio, obtenemos: $\overline{X_1}= 4.62164$

Si tomamos una segunda muestra, con los valores: 8.5333600 0.4704488 5.8710375 6.0414564 4.5583983 9.7168667 6.7065967 2.2844655 3.7532787 9.9928106

Obtenemos el promedio $\overline{X_2}=5.792872$

Si tomamos una tercera muestra, con valores: 0.5721976 3.5036649 2.5889360 1.2619283 7.1515359 2.5302950 2.7476769 6.1138531 6.5134797 0.7043770

Obtenemos: $\overline{X_3} =3.368794$

Fíjese que esos promedios son distintos. Queremos saber cuál puede ser un buen valor del promedio (estadístico de centro) y de su desviación estándar.

Segun el Teorema del Límite Central, $\{\overline{X}\}$ tiene una distribución normal, y su $\mu$ es el de la distribución original. Su desviación estándar es $\sigma/\sqrt{n}$, es decir, teniendo la desviación estándar de la distribución de muestreo podemos calcular la de la distribución original.

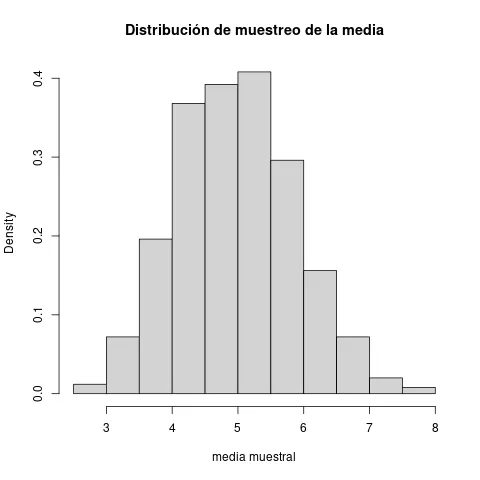
En este caso la siguiente es la distribución de promedios. ¿que puede decir del promedio de los promedios, comparado con el promedio de la distribución original?

Tarea

• Continuar la lectura hasta la página 252.
• Ejercicios página 252.

Resumen

• El objetivo es encontrar los parámetros, $\mu$ y $\sigma$, que caracterizan una distribución

• No es posible (muy caro, muy difícil técnicamente) hacer un censo. Si se pueden tomar un número $k$ de muestras ${X_i}$, de tamaño $n$.

• Cada muestra ${X_i}$ puede llevar a un promedio $\overline{X}$.

• El teorema del límite central indica que una aproximación a $\mu$ es tomar un promedio de los promedios, $\mu \approx \overline{\overline{X}}$

• El teorema del límite central indica que una aproximación a $\sigma$ es tomar la desviación estándar de los promedios y multiplicar por la raíz del tamaño de la muestra: $\sigma \approx S_{\overline{X}} \sqrt{n}$

Ejemplo

• Queremos caracterizar el consumo calórico de estudiantes de pregrado de las universidades.

• Es muy difícil ponerle una cámara espía a todas las personas (censo), es ilegal (no todas aceptan), preguntarles que comieron no es tan preciso (olvidan). Entonces se decide tomar varias muestras (grupos de personas) a quienes se les pone la cámara espía (voluntariamente) para registrar consumo calórico.

• Sobre cada muestra se calcula un promedio.

• El teorema del límite central permite estimar el promedio de la distribución del consumo calórico como el promedio de los promedios.

• El teorema del límite central permite estimar la desviación estándar como la desviación estándar de los promedios, multiplicado por la raíz del tamaño de la muestra.

Simulación de la distribución de muestreo

Construimos una simulación de la distribución de muestreo, siguiendo el ejemplo del libro de Contento (aunque aquí en Python, no en R).

Ojo: recuerde que los bloques de la estructrua for requieren que las instrucciones tengan la misma sangría y estén en el mismo bloque de código. Y se recomienda agrupar instrucciones que tengan funcionalidad similar por bloques.

Incluimos las librerías e iniciamos la semilla del generador:

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(3)

Ingresamos los parámetros, tanto de la distribución que vamos a estudiar, como $n$, tamaño de muestras y $k$, número de muestras.

miu = 10
sigma = 3

n = 3
k = 4

Generamos arreglos donde guardar promedios $\overline{X}$ y muestras ${X_i}$

promedios = np.zeros(k)
mat = np.zeros((k,n))  # Arreglo de k vectores cada uno de tamaño n

Aquí recomendamos imprimir las variables promedios y mat, para que veámos cómo es su estructura. ¡hágalo!

El bloque que genera las muestras, calcula los promedios y los guarda es el siguiente:

for i in range(k):
    muestra = np.random.normal(miu,sigma,n)
    mat[i] = muestra
    promedios[i] = np.mean(muestra)

De nuevo, imprima las variables promediosy mat para que vea cómo se llenaron.

Ahora, vuelva atrás en su código y cambie los valores de n y k a 25 y 100 respectivamente. Los valores anteriores eran de prueba, para revisar cómo estaba guardando los datos. Con los nuevos valores de ny k, vuelva a correr el código.

Para generar una figura de los histogramas de tres muestras:

plt.figure()
plt.title("tres muestras")
plt.hist(mat[k-3],alpha=0.7,label='muestra '+str(k-3)+ ' $\overline{X}=$ '+str(round(promedios[k-3],3)))
plt.hist(mat[k-2],alpha=0.7,label='muestra '+str(k-2)+ ' $\overline{X}=$ '+str(round(promedios[k-2],3)))
plt.hist(mat[k-1],alpha=0.7,label='muestra '+str(k-1)+ ' $\overline{X}=$ '+str(round(promedios[k-1],3)))
plt.legend()
plt.xlabel(r'''$x_i$''')
plt.ylabel(r'''$N(X)$''')

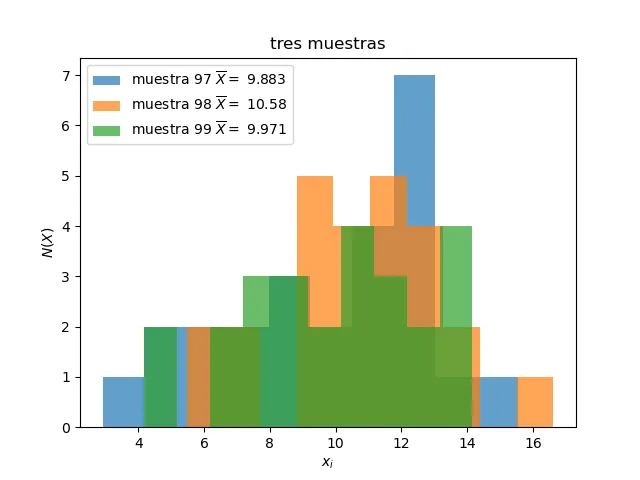
Podemos también generar un histograma de los promedios, llamado distribución de muestreo del promedio.

plt.figure()
plt.hist(promedios,color='r')
plt.title("Distribución de  Muestreo")
plt.xlabel(r'''$\overline{x}$''')

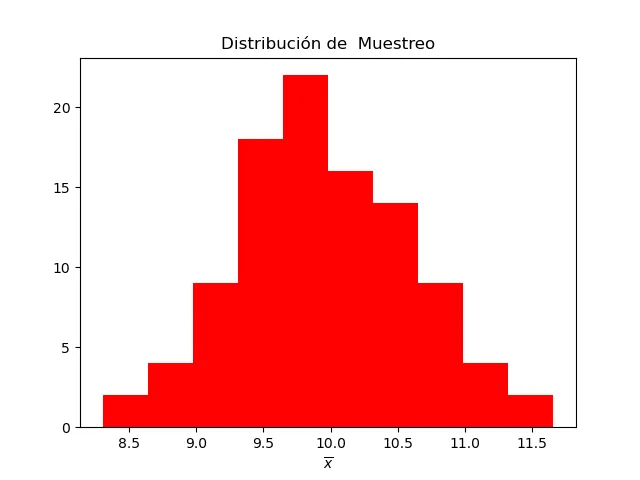
También podemos imprimir los valores

print("el promedio es " + str(np.mean(promedios)))
print("la desviación estándar es " + str(np.std(promedios)))

Taller en clase

Haremos los ejercicios de la página 243 en la siguiente clase.