Table of contents

Distribuciones de Probabilidad y Estimación de Parámetros

Distribución Binomial

${\color{blue} Contento, \ pg.\ 176}$ ${\color{red} González,\ pgs. 264 \ a\ 271}$

Ejemplo: aves marcadas

(Contento, pg 176)

Suponga que en una población de aves aproximadamente el 5% de los animales han sido marcados. Se capturan 2 especímenes de esas aves (por ejemplo, para pesarlos querríamos que estén marcados; o para marcarlos, luego querríamos que no estén marcados).

1. ¿Cuál es la probabilidad de que, atrapando 1, 1 esté marcado?
2. ¿Cuál es la probabilidad de que, atrapando 2, 2 estén marcados?
3. ¿Cuál es la probabilidad de que, atrapando 2, 1 esté marcados?
4. ¿Cuál es la probabilidad de que, atrapando 2, 0 esté marcados?

Respuesta

1. Cómo el 5% están marcados, la probabilidad de que uno elegido al azar esté marcado es de 0.05

2. Aquí construimos la siguiente tabla:

Experimento Binomial

• Consta de $n$ pruebas idénticas
• Cada prueba tiene sólo dos resultados: Éxito o Fracaso
• La probabilidad de éxito es $p$, no cambia entre pruebas. La probabilidad de fracaso es $q=1-p$.
• Las pruebas son independientes
• La variable aleatoria es: $X$ # de éxitos

Función Binomial de Probabilidad

Si una variable aleatoria es un experimento binomial $x\sim B(n;p)$, su función de distribución de probabilidad es:

$P(x) =\begin{pmatrix} n \\ x \end{pmatrix} p^x q^{n-x} \ \ x=0,1,...,n$

Se requiere saber $n$ y $p$.

Promedio y Varianza de una Binomial

Si $x\sim B(n;p)$ entonces:

$\mu = n \cdot p$

$\sigma^2 = n \cdot p \cdot q$

Ejemplo: Deducible de un seguro

Una empresa de seguros tiene una póliza que tiene un monto mínimo para hacer válidos los pagos (deducible). Concluyó que la probabilidad de que una persona al azar supere el deducible es del 0.3. ¿Con qué probabilidad 3 de 8 individuos hayan superado el deducible?

¿Cumple las condiciones?

• Consta de $n$ pruebas idénticas¹
• Cada prueba tiene sólo dos resultados: Éxito o Fracaso²
• La probabilidad de éxito es $p$, no cambia entre pruebas ³. La probabilidad de fracaso es $q=1-p$.
• Las pruebas son independientes⁴
• La variable aleatoria es: $X$ # de éxitos

¿cual es la probabilidad?

Se trata de una binomial, con $n=8$, $x=3$, $p=0.3$, luego se trata de una $B(3;0.7). Tendríamos:

$P(3) =\begin{pmatrix} 8 \\ 3 \end{pmatrix} 0.3^3 0.7^{5} = 8*7*0.3^3*0.7^5 \approx 0.2541$

En Python:

8*7*0.3**3*0.7**5

O usando la función binom.pmf de la librería scipy.stats:

import scipy.stats as stats
stats.binom.pmf(3,8,0.3)

Ejemplo

Un experimento binomial tiene 4 repeticiones idénticas. La probabilidad de éxito es de $0.7$. ¿Cuál es la probabilidad de que haya respectivamente 0,1,2,3,4 éxitos?

Podríamos construir un diagrama de árbol:

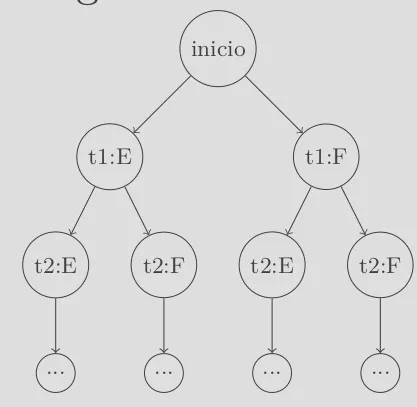
Por ejemplo para $x=4$ sólo hay una rama, con $P=0.7\cdot0.7\cdot0.7\cdot0.7 = 0.7^4 \cdot 1 = 0.7^4 \cdot 0.3^0 = 0.2401$

Ahora, el cálculo es el de una binomial con $n= 4$, y $p= 0.7$, con $P(x) =\begin{pmatrix} n \\ x \end{pmatrix} p^x q^{n-x}=\frac{n!}{x!(n-x)!}p^x q^{n-x}$

Luego:

• $P(4) = \begin{pmatrix} 4 \\ 4 \end{pmatrix} (0.7)^4 (0.3)^{0} = 0.2401$

• $P(3) = \begin{pmatrix} 4 \\ 3 \end{pmatrix} (0.7)^3 (0.3)^{1} = \frac{4\cdot 3\cdot 2 \cdot 1 }{3\cdot 2 \cdot 1 \cdot 1} \cdot (0.7)^3 (0.3)^{1} = 0.4116$

• $P(2) = \begin{pmatrix} 4 \\ 2 \end{pmatrix} (0.7)^2 (0.3)^{2} = \frac{4\cdot 3\cdot 2 \cdot 1 }{2\cdot 1 \cdot 2 \cdot 1} \cdot (0.7)^2 (0.3)^{2} = 0.2646$

• $P(1) = \begin{pmatrix} 4 \\ 1 \end{pmatrix} (0.7)^1 (0.3)^{3} = \frac{4\cdot 3\cdot 2 \cdot 1 }{1 \cdot 3 \cdot 2 \cdot 1} \cdot (0.7)^1 (0.3)^{3} = 0.0756$

• $P(0) = \begin{pmatrix} 4 \\ 0 \end{pmatrix} (0.7)^0 (0.3)^{4} = \frac{4\cdot 3\cdot 2 \cdot 1 }{1\cdot 4 \cdot 3 \cdot 2 \cdot 1} \cdot (0.7)^0 (0.3)^{4} = 0.0081$

Y $P(4)+P(3)+P(2)+P(1)+P(0) = 1$, $\mu = n\cdot p = 4 \cdot 0.7 = 2.8$, y $\sigma^2 = n\cdot p \cdot q = 4\cdot 0.7 \cdot 0.3 = 0.84$.

Ejemplo ${\color{blue} Contento \ pg. \ 178}$

La solución se puede encontrar las hojas de cálculo, usdando las funciones propias de éstos sistemas. Ahora, es una binomial con $n= 4$, y $p= 0.7$, con $P(x) = \begin{pmatrix} n \\ x \end{pmatrix} p^x q^{n-x}=\frac{n!}{x!(n-x)!}p^x q^{n-x}$

Cálculo en el software

Usando Hojas de Calculo, por ejemplo libreoffice, la función es binom.distr(X,trials,SP,C), donde X es el número de éxitos, trials el número de repeticions, SP la probabilidad y C indica si es acumulativo o no. En este caso:

• $P(0)$: binom.distr(0,4,0.7,0) $=0.0081$
• $P(1)$: binom.distr(1,4,0.7,0) $=0.0756$
• $P(2)$: binom.distr(2,4,0.7,0) $=0.2646$
• $P(3)$: binom.distr(3,4,0.7,0) $=0.4116$
• $P(4)$: binom.distr(4,4,0.7,0) $=0.2401$

Usando Python, la función es binom.pmf de la librería scipy.stats. Por ejemplo para el primer valor tenemos:

import scipy.stats as st
st.binom.pmf(0,4,0.7)

El software devuelve el valor $0.008100000000000005$.

Usando R, la función es dbinom. Aquí la instrucción sería:dbinom(0,4,0.7), y se obtiene como respuesta el valor $0.0081$.

Una vez tenemos todos los valores, podemos graficarlos:

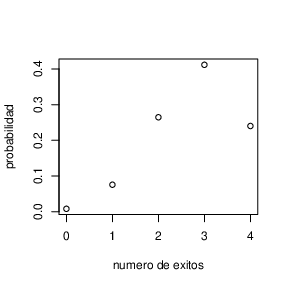
Ejercicios

• “Cuatro jueces…” ${\color{blue} Contento \ pg. \ 180}$
• ${\color{red} González, \ ejercicios \ 5.1,\ página \ 271}$

Distribución de Poisson

${\color{red}\ González,\ pg.\ 275\ a\ 278}$

${\color{blue} Contento,\ pg.\ 185}$

• Los eventos son infrecuentes
• Los eventos dependen de otra cantidad (como distancia, área, volúmen, tiempo)
• La prbobabilidad por unidad de esa cantidad es constante. (densidad de probabilidad?)
• El número de eventos en un intervalo es independiente de los que ocurren en otros.

Ejemplos

• Árboles caídos por $km^2$
• Vehículos en una intersección cada minuto
• Clientes que asisten a una oficina cada hora.

En las Hojas de cálculo

La distribución de Poisson $P(x,\mu)$ se calcula usando POISSON.DIST(x,lambda,cumm). x el # de éxitos, lambda es $\mu$, y cumm un valor lógico que vale $0$ si no es la distribución acumulada, $1$ si es.

Densidad de probabilidad Poisson

La función de probabilidad de una variable aleatoria distribuida como Poisson es:

$P(x) = \frac{e^{-\mu} \mu^x}{x!}$

$x=0,1,2,...$

Donde $\mu$ es el promedio de ocurrencias fenómeno cada unidad. La variable se distribuye como Poisson: $X\sim P(\mu)$

Promedio y Varianza

Si $X\sim P(\mu)$ es una variable aleatoria distribuida Poisson, entonces $E(X) = V(X) = \mu = \sigma^2$.

Ejercicios

En Khan Academy:

Recursos Adicionales

Notas a pie