Table of contents

Tipos de distribuciones

Distribuciones Continuas

Variable continua

Las variables continuas toman valores en los números reales. Representan cantidades cuya medición puede ser un valor decimal,

Ejemplo: variable peso-al-nacer

En una base de datos se registran el peso al nacer de los neonatos. Se pesan con una balanza con una precisión de 0.001 kg (es decir 1g); por lo tanto la variable “peso del neonato” es continua.

Función de densidad de probabilidad de una variable continua

Cuando la variable es continua, no tiene sentido hablar de la probabilidad de que se obtenga un valor exacto. En su lugar se habla de la probabilidad de que una variable tome un valor en un intervalo. La función densidad de probabilidad tiene las siguientes características:

• $f(x) \geq 0$ La función de probabilidad es positiva.

• $\int_{-\infty}^{\infty} f(x) dx = 1$. El área bajo la curva de la densidad de probabilidad es 1.

• $P(a \leq X \leq b) = \int_a^b f(x) dx$. La probabilidad de un evento entre $a$ y $b$ es la integral entre esos dos valores.

Distribución uniforme continua

Dada una variable $X$, que puede tomar valores en el intervalo $[a,b]$, entonces la densidad uniforme contínua es:

$f(x) = \frac{1}{b-a}\ \ ; \ \ a \leq x \leq b$

La notación $X \sim U_c(a,b)$ se lee: x se distribuye uniforme contínua en el intervalo a,b

• Valor esperado de la distribución uniforme continua $\mu = \frac{b+a}{2}$
• Varianza de la distribución uniforme continua $\sigma^2 = \frac{(b-a)^2}{12}$

Ejemplo: Contaminante (contento, pg. 198)

La concentración de cierto contaminante está distribuida de manera uniforme en el intervalo $0$ a $20$ ppm. Si se considera tóxica una concentración de $8$ o más, responda las preguntas:

• ¿Con qué probabilidad al tomarse una muestra se encuentra una concetración tóxica?

• ¿Cuál es la concentración media? ¿la varianza?

• ¿Con qué probabilidad la concentración es exactamente $10$?

Ejemplo: Probabilidad lineal

Supongamos que la densidad de probabilidad está dada por la siguiente función:

$p(x) = -0.125 x + 0.5 \ ; \ 0 < x < 4$

Representada por la siguiente gráfica:

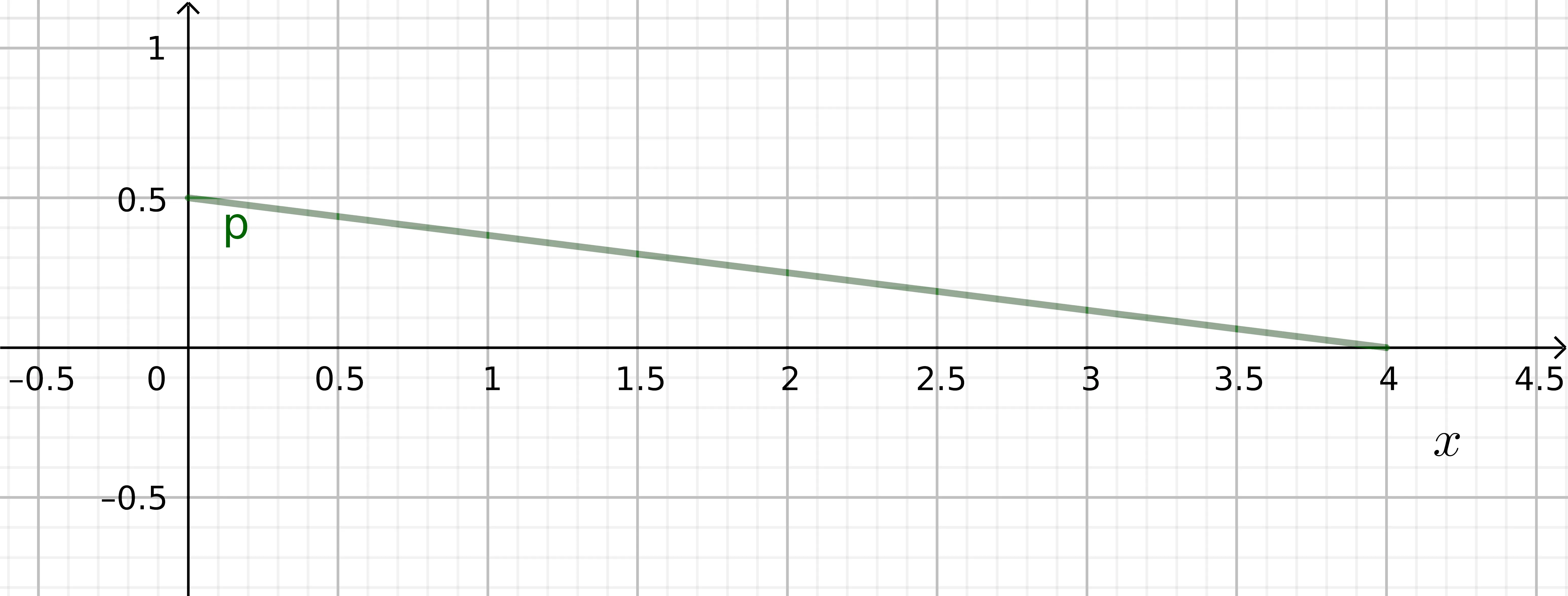Si quisieramos hallar la probabilidad de que la variable $x$ tome valores entre 0 y 1, por ejemplo, se requiere la integral:

$P(0\leq X \leq 1) = \int_0^1 (-0.125 x + 0.5) dx$

$P(0\leq X \leq 1) = (-0.125 \frac{x^2}{2} + 0.5 x ) |_0^1$

$P(0\leq X \leq 1) = (\frac{-0.125}{2} + 0.5 ) = 0.4375$

La probabilidad de que la variable $X$ tome valores entre $0$ y $1$ es de $0.4375$

Distribución binomial (repaso)

Supongamos que se lanza una moneda 100 veces, y se registra el resultado como +1 si se obtiene cara y -1 si se obtiene sello. Nos preguntamos:

• ¿Qué valores se pueden obtener en la suma?

• ¿Qué valor es más probable?

• ¿Que características tiene la distribución de probabilidad de la variable “suma”?

Podemos decir que se trata de una distribución binomial. Los valores que puede tomar la suma van de -100 (si todas son sellos) a +100 (si todas son caras. La situación más probable es que la suma sea 0, es decir que haya tantos valores de cara como de sello. Y sabemos que la distribución será simétrica, es decir la probabilidad de que la suma sea igual a 1 es idéntica a que sea -1, y así sucesivamente.

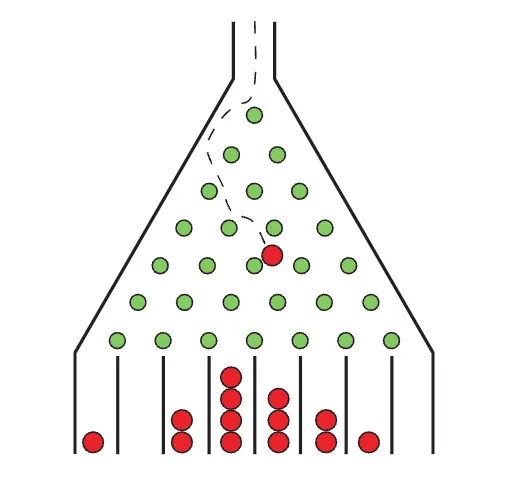
Distribución gaussiana (normal)

Existen variables continuas que tienen características similares a las de la binomial. Es el caso de las variables morfológicas (forma). Si pensamos por ejemplo en el peso al nacer de neonatos de una misma generación, se espera que el valor más común sea el promedio, y que a medida que nos alejamos del promedio se reduzca la probabilidad.

La distribución gaussiana tiene las siguientes características:

• Está definida por dos parámetros, que son su promedio $\mu$ y su desviación estándar $\sigma$.

• La variable es un continua: $X \in \mathcal{R}$

• La distribución $f$ es simétrica

• Su mediana es igual a su moda

• Asintótica al eje x (se acerca a cero).

• Tiene la siguiente forma funcional:

  $f(x) = \frac{1}{\sqrt{2 \pi \sigma}}e^{-\frac{1}{2} \left( \frac{x - \mu}{\sigma}\right)^2},$

  Aquí $\sigma$ es la desviación estándar, $\mu$ el promedio. Es una función exponencial. (Ayuda: aunque parece rara, usualmente se calcula con computadoras.)

• Distribución Gaussiana Estandar: Para simplificar la forma funcional y poder realizar cálculos sin computadora, se ha estudiado la Gaussina que tiene $\mu = 0$, $\sigma = 1$. Es:

  $f(z) = \frac{1}{\sqrt{2 \pi }}e^{-\frac{1}{2} z^2},$

Simulación de la distribución gaussiana

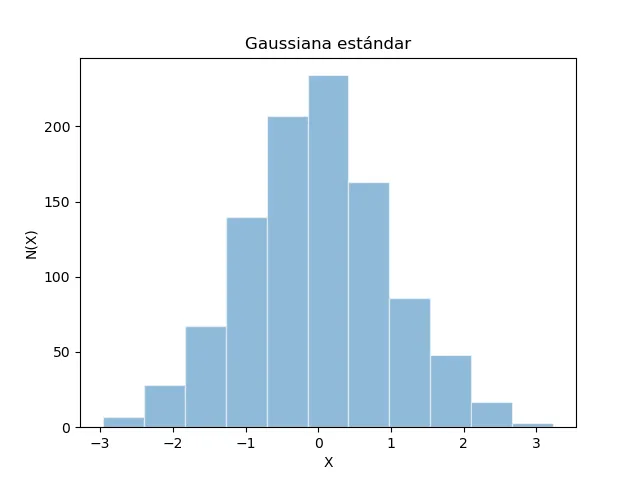
Se usa la función random.normalde la librería numpy. En la ayuda se tienen tres argumentos: loc, scale y size: normal(loc=0.0, scale=1.0, size=None). Corresponden al centro de la distribución, $\mu$; la desviación estándar, $\sigma$ y el tamaño de la muestra $N$. La distribución gaussiana ** estandar** tiene $\mu =0$ y $\sigma = 1$. Por ejemplo:

import numpy as np
muestra = np.random.normal(0,1,1000)
plt.hist(muestra,bins=11,edgecolor='w',alpha=0.5)
plt.xlabel("X")
plt.ylabel("N(X)")
plt.title("Gaussina estandar")

Se obtiene la siguiente gráfica:

Ejercicio en clase, diferentes distribuciones gaussianas.

Seguimos con $N=1000$.

• Haga una gráfica que tenga tres simulaciones. Las muestras deben ser gaussianas con $\sigma =1$, pero centradas respectivamente en $-2$, $0$ y $2$.

• Haga una gráfica que tenga tres simulaciones. Las muestras deben ser gaussianas con $\mu=1$, pero con diferentes valores de la varianza, $\sigma=1$, $\sigma=2$ y $\sigma=4$. Incluya la variable density=True en el plot: plt.hist( ... ,density=True). Ojo, esta instrucción está incompleta, debe reemplazar los ... por las instrucciones que usted conoce.

Estandarización

Es un proceso para comparar distribuciones que tienen diferentes parámetros, pero que tienen la misma forma. Recordemos que la forma funcional de la gaussiana es $f(x) = \frac{1}{\sqrt{2 \pi \sigma}}e^{-\frac{1}{2} \left( \frac{x - \mu}{\sigma}\right)^2},$; fíjese que la variable $X$ aparece acompañada de $\mu$ y $\sigma$ de la forma $\frac{x - \mu}{\sigma}$. La estandarización consiste en definir una nueva variable $Z$:

$Z = \frac{x - \mu}{\sigma}$

El valor $Z$ determina la distancia, medida en desviaciones estándar, desde el promedio. Es positiva si está a la derecha del promedio y negativa si está a su izquierda.

Por la forma que tiene la distribución gaussiana, Z usualmente varía entre -3 hasta 3; es decir de 3 desviaciones estándar a la izquierda hasta 3 desviaciones estándar a la derecha.

Ejemplo, comparando resultados de dos exámenes

(fuente: Diez, D. M., Barr, C. D., & Cetinkaya-Rundel, M. (2012). OpenIntro statistics, página 134)

Supongamos que tenemos dos poblaciones a las que se les hacen exámenes diferentes, pero que tratan de medir lo mismo. Pueden ser exámenes saber 11 de dos años diferentes, que tratan de evaluar lo mismo pero resultan que en la práctica uno es más difícil que el otro. ¿cómo se pueden comparar los resultados personas que hicieron diferentes examenes?

• Ana tiene un puntaje sin estandarizar de 370, y en su grupo el promedio fue de 350 con una desviación estándar de 20.

• Juan tiene un puntaje sin estandarizar de 370, en su grupo el promedio fue de 360, con una desviación estándar de 5.

Cómo se puede comparar el puntaje de Ana con el de Juan?

La gráfica muestra distribución del grupo de Ana, en naranja; y la distribución del grupo de Juan, en azul.

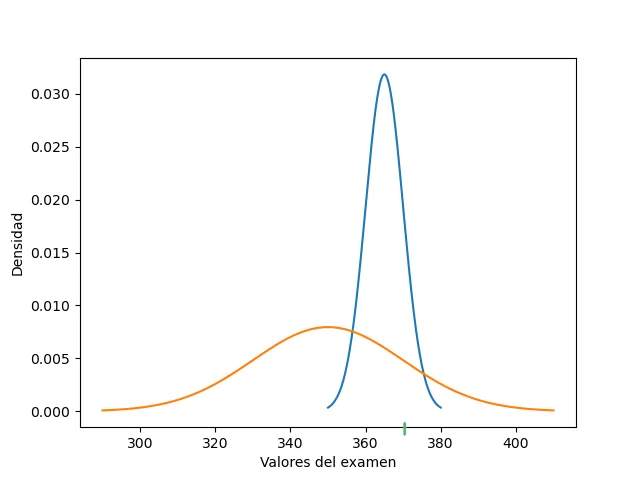
Aunque ambos tuvieron el mismo puntaje sin estandarizar, hay una mayor variabilidad en el grupo de Ana que en el grupo de Juan. Para compararlos usamos el valor $Z$.

$Z_{Ana} = \frac{370-350}{20} = \frac{20}{20} = 1$

$Z_{Juan} = \frac{370-360}{5} = \frac{10}{5} = 2$

Ambos están a la derecha del promedio, pero Ana está sólo a una desviación estándar del promedio; mientras que Juan está a dos desviaciones estándar del promedio. En comparación a sus grupos, es decir a las situaciones que les correspondió a cada uno, por ejemplo en términos de que tan difícil fue su examen, Juan tiene una mejor valoración que Ana.

Tabla Gaussiana Estandar

Reporta las probabilidades acumuladas hasta un $z_0$ dado. Es decir, calcula $P(Z\leq z_0) = \int_{-\infty}^{z_0} \frac{1}{2\pi \sigma} e^{\frac{-1}{2}z^2} dz$. Es el área de la siguiente gráfica.

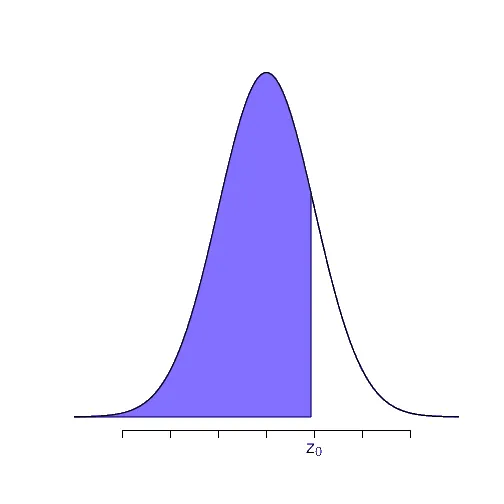
Ejemplo

Supongamos que queremos encontrar la probabilidad de que la variable $Z$ tenga un valor menor a $-2.05$. Eso equivale a encontrar el área bajo la curva desde $-\infty$ hasta $-2.05$. Esa área correspondería gráficamente a la siguiente área marcada con violeta:

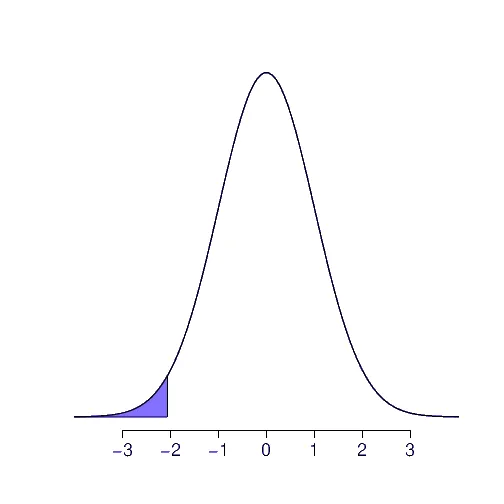
Para encontrar esta probabilidad con el software se usa la tabla. Se buscan las unidades y el primer decimal en la primera columna y el segundo decimal en la primera fila, así:

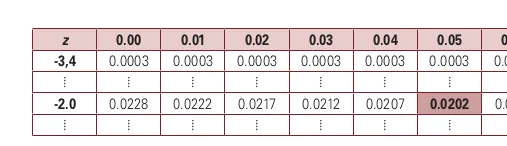
Probabilidad a cola derecha

La probabilidad a cola derecha corresponde al área acumulada a partir de un valor. Por ejemplo, la siguiente figura representa la probabilidad $P(Z\geq 2.0)$:

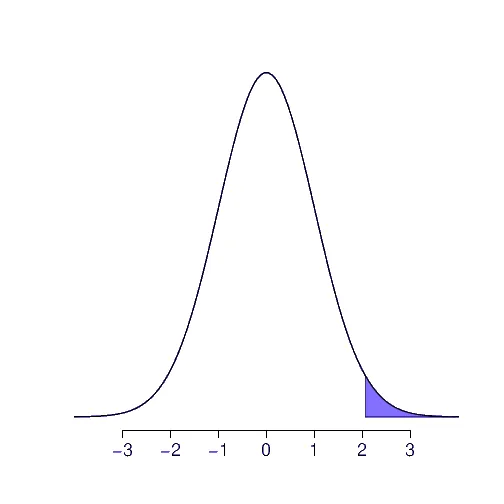
Ahora, en las tablas está la probabilidad a cola izquierda. Luego lo que se hace es buscar el evento complementario $\overline{A}$, y calcular su probabilidad. El complemento del evento $A:Z>2.0$ es el evento: $\overline{A}:Z\leq 2.0$

Luego:

$P(A) = 1- P(\overline{A})$

$P(Z>2.0) = 1- P(Z \leq 2.0)=0.0228$

En Python

Se importa la librería statsde scipy:

import scipy.stats as st

Por ejemplo, para la probabilidad acumulada $P(Z \leq -2.05)$, se haría:

st.norm.cdf(-2.05)

Lo que da el valor: 0.020182215405704394, se puede aproximar a cuatro decimales en 0.0202.

Para $P(Z>2)$:

1-st.norm.cdf(2)

Se obtiene 0.02275013194817921 o aproximando a cuatro decimales 0.0227.

Punto crítico

Es el valor $z=z_{\alpha}$ tal que la probabilidad $P(Z>z_{\alpha}) = \alpha$. Se representa en la siguiente gráfica por el valor $z_0$

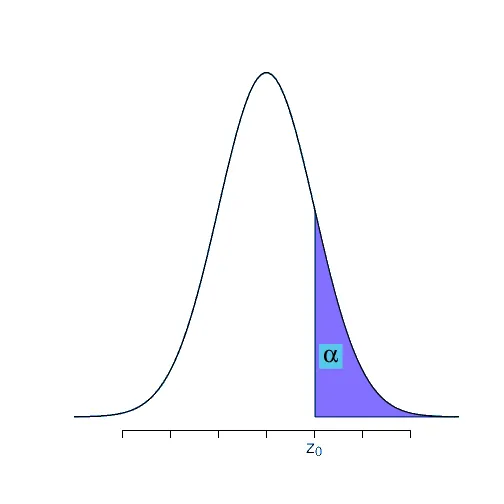
Es decir, si antes teníamos el valor $z_0$ y hallabamos la probabilidad $\alpha$, ahora tenemos la probabilidad a cola derecha y buscamos el valor $z_0$.

Para hacerlo usando la tabla de probabilidades, como la tabla tiene probabilidad a cola izquierda y aquí queremos a cola derecha, usamos la probabilidad del evento complementario. Es decir buscamos en la tabla el valor $z$ que corresponde a la probabilidad $1-\alpha$.

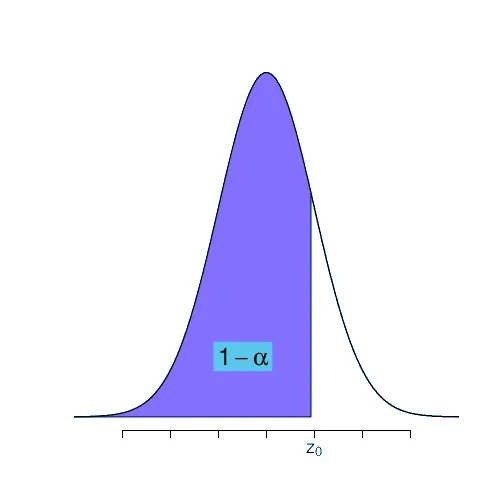
Ejemplo

¿Que $z_{0}$ hace que $P(Z>z_0) = 0.8413$?

Tomamos $P(Z\leq z_0) = 1-0.8413 = 0.1587$

Según la tabla:

El valor sería de -1. Este es un valor aproximado, si se calcula con el software se tiene:

st.norm.ppf(0.1587)

Lo que devuelve el valor $-0.999815093614744$.

Bibliografía

• la imágen de la máquina de Galton está en mathoverlow: https://mathoverflow.net/questions/419706/placing-pins-on-a-galton-board-to-approximate-an-arbitrary-distribution

• La función ppf de scipy.stats https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.rv_continuous.ppf.html

• La función cdf de scipy.stats https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.rv_continuous.cdf.html

• Ejemplo en stackoverflow https://stackoverflow.com/questions/20864847/probability-to-z-score-and-vice-versa