Anteriormente trabajamos el tema de los diferentes enfoques de probabilidad. Aquí vamos a construir algunos ejemplos para desarrollar los conceptos.

Archivo para entregar

En grupos de 2 personas.

Reglas para el nombre del archivo

• Comienza con la fecha en formato ISO
• Incluye los primeros apellidos de cada persona del grupo, en mayúscula
• No tiene espacios, en lugar usa barra al piso

Formato del archivo

Puede hacerlo en google colab (nuevo proyecto) o en Anaconda. El archivo que entregue debe ser un .ipynb. 🆕

Nombres, correos

Incluya en el texto del archivo los nombres completos de quienes componen el grupo y sus direcciones de correo electrónico

Explicación a sus respuestas

Dentro del texto del archivo use los comentarios, con el símbolo #, para incluir comentarios, que expliquen lo que está haciendo y que respondan las preguntas que sean teóricas.

También puede hacerlo usando bloques de texto en el cuaderno de jupyter. Identifique el número de la pregunta y los valores particulares (por ejemplo $N$ ). 🆕

Bloques de instrucciones

Es mejor si incluye varias instrucciones en un sólo bloque de instrucciones, en lugar de un bloque para cada instrucción

Ejemplo

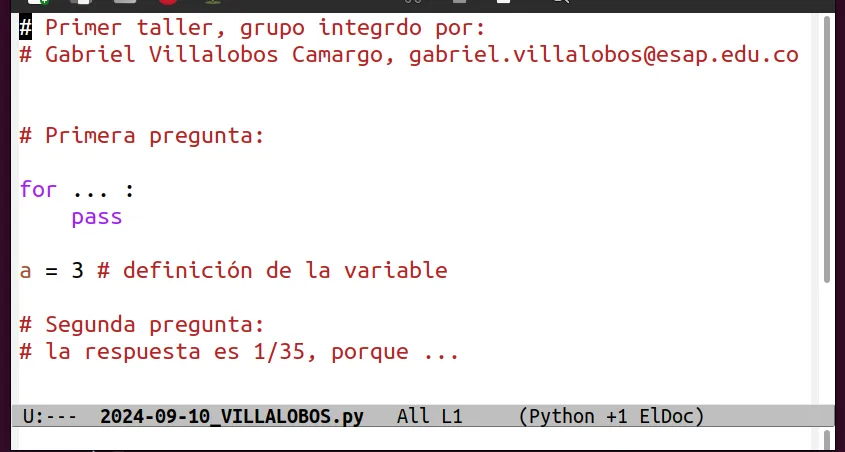
Python: librerías

Para incluir una librería se usa el comando import, seguido por el nombre de la librería. Para usar un alias (usualmente acordar) se usa el comando as, seguido por el alias. Por ejemplo, para uasar la librería numpy, con el alias np, se escribiría el comando:

import numpy as np

Vamos a utilizar las siguientes librerías:

• numpy, con el alias np
• random, con el alias ran
• matplotlib.pyplot, con el alias plt

numpy

Es la librería numérica de python. Usualmente se incluye con el alias np. Se importa como:

import numpy as np

np.linspace

Lo usamos para generar números en un intervalo. Por ejemplo, np.linspace(0,10,11) genera los números del $0$ al $10$. Devuelve un arreglo.

random

Tiene funciones para números aleatorios. Se usa el alias ran. Se importa como:

import random as ran

semilla

Los generadores de números aleatorios realmente no son verdaderamente aleatorios, siguen reglas definidas que pareciera que generan números completamente aleatorios. Ahora, durante la fase de escritura y revisión del código es útil que las funciones generadoras de números aleatorios parezcan aleatorias pero repitan siempre la misma secuencia de números cada vez que se corre de nuevo el código.

Para garantizar que cada vez que se usa el código se generan los mismos valores aleatorios se usa una semilla, que es un valor numérico. Por ejemplo, el código:

ran.seed(3)

Define que la semilla es el número 3.

ran.choice

Lo usamos para elegir elementos al azar, por ejemplo de un arreglo.

Ejemplo

El siguiente código simula un único lanzamiento de un dado de seis caras:

import random as ran
ran.seed(8)
unlance = ran.choice([1,2,3,4,5,6])

• Se avisa que va a usar la librería random, usando el alias ran
• Usa una semilla, en este caso el número 8
• Elige ‘al azar’ un número entre los enteros del 1 al 6, y lo asigna a la variable unlance

matplotlib.pyplot

Matplotlib es la librería que se usa para generar las gráficas. Se suele importar con el alias plt:

import matplotlib.pyplot as plt

plt.hist

Lo usamos para construir un histograma. Vamos a usarlo con cuatro argumentos. El primero, la lista de valores que van en el histograma. El segundo, el rango, una pareja de números para un histograma de enteros como pareja el 1 y el máximo + 1. El tercero la palabra clave bins igual al número de opciones del dado, cuarto la palabra clave density en True, para que se genere un histograma normalizado.

Por ejemplo, si estamos simulando un dado de tres valores, $1,2,3$, y los datos que se obtuvieron del lanzamiento del dado son:

datos = [1,1,2,3,1,3,2,1,1,3,2,1,2]

El histograma se genera así:

plt.hist(datos,range=(1,3),bins=3,density=True)

Taller

Vamos a simular el lanzamiento de un dado de un número diferente de caras ($N$) cada grupo de estudiantes. Lo deben analizar de dos formas, tanto como probabilidad clásica, como probabilidad como frecuencia relativa.

Forme un grupo de 2 estudiantes, informe los miembros al profesor, que le asignará el valor de $N$ para su grupo.

1. Probabilidad clásica.

Responda la siguiente pregunta usando la definición clásica de probabilidad: ¿cuál es la probabilidad clásica de que al lanzar el dado se obtenga el valor de 1?

2. Probabilidad como frecuencia relativa

• Defina una lista vacía, llamada ldatos (más adelante la usará para ir añadiendo los valores que genera en el dado)
• Usando un for, repita 1000 veces la instrucción que representa el lanzamiento del dado con el valor máximo que se le asignó. Añada el resultado del dado a la lista ldatos
• Genere la gráfica.

3. Compare

Compare el valor de la probabilidad clásica con el que obtuvo como frecuencia relativa. ¿que concluye?

Rúbrica 🆕

• Órden y seguir reglas: +0.5
• Pregunta 1: +1.5
• Pregunta 2: +1.5
• Pregunta 3: +1.5