Table of contents

Repaso

Estructuras

Hemos visto las siguientes estructuras de datos:

• variables numéricas, como por ejemplo unNumero = 3
• texto, como por ejemplo ciudad = "Guadalajara"
• listas, como por ejemplo nombres = ["luis","diana","carlos"]

Funciones

Instrucciones que realizan operciones sobre un argumento.

• imprimir: print, su argumento es un texto que va entre paréntesis; ejemplo: `print(“Hola Mundo”)
• funciones de las mismas estructuras, afectan una estructura que hayamos definido; ejemplo: ciudad.upper() devuelve el resultado de escribir en mayúsculas el contenido de la variable ciudad.

Operaciones

Son similares a las operaciones matemáticas que están implementadas en las calculadoras, como por ejemplo la suma, multiplicación, potencia, etc. Aunque en programación se extiende a manipulaciones con las cadenas de texto.

Ejemplos:

• Suma entre números 1 + 35
• Unir dos cadenas de texto "1" + "35"

Librerías

Son conjuntos de instrucciones que expanden las posibilidades del software original

Incluir una librería

Se usa el comando import, seguido del nombre de la libería, luego la palabra clave asy luego un alias. Por ejemplo:

import numpy as np

Importa la librería numpy y le da el alias de np. Esta es la que vamos a usar en este ejercicio en clase.

Ayuda sobre las funciones

Python tiene una forma de dar ayuda sobre las funciones que están incluidas. Para acceder a la ayuda de una función, use el operador ? después de la función y ejecute el código.

Por ejemplo para acceder a la ayuda de la función print se telearía lo siguiente:

print?

Al ejecutar el código nos aparece a la derecha la ayuda de la función.

Primer ejercicio en clase

Este ejercicio en clase no entra en las calificaciones del corte

Instrucciones

El objetivo de este ejercicio en clase es que ustedes desarrollen los conceptos que vimos en la clase anterior. Por lo tanto:

• No busque la respuesta en internet
• Está Explícitamente prohibido uso de LLMs: ❌ 💫
• Cualquier duda, pregunte!

Reglas para el nombre del archivo

• Comienza con la fecha en formato ISO (ejemplo: 2025-02-09, para el 9 de ferero de 2025)
• Incluye los primeros apellidos de cada persona del grupo, en mayúscula
• No tiene espacios, en lugar usa barra al piso

Formato del archivo

Puede hacerlo en google colab (nuevo proyecto) o en Anaconda. El archivo que entregue debe ser un .ipynb. 🆕

Nombres, correos

Incluya en el texto del archivo los nombres completos de quienes componen el grupo y sus direcciones de correo electrónico

Explicación a sus respuestas

Dentro del texto del archivo use los comentarios, con el símbolo #, para incluir comentarios, que expliquen lo que está haciendo y que respondan las preguntas que sean teóricas.

También puede hacerlo usando bloques de texto en el cuaderno de jupyter. Identifique el número de la pregunta y los valores particulares (por ejemplo $N$ ). 🆕

Bloques de instrucciones

Es mejor si incluye varias instrucciones en un sólo bloque de instrucciones, en lugar de un bloque para cada instrucción

Ejemplo

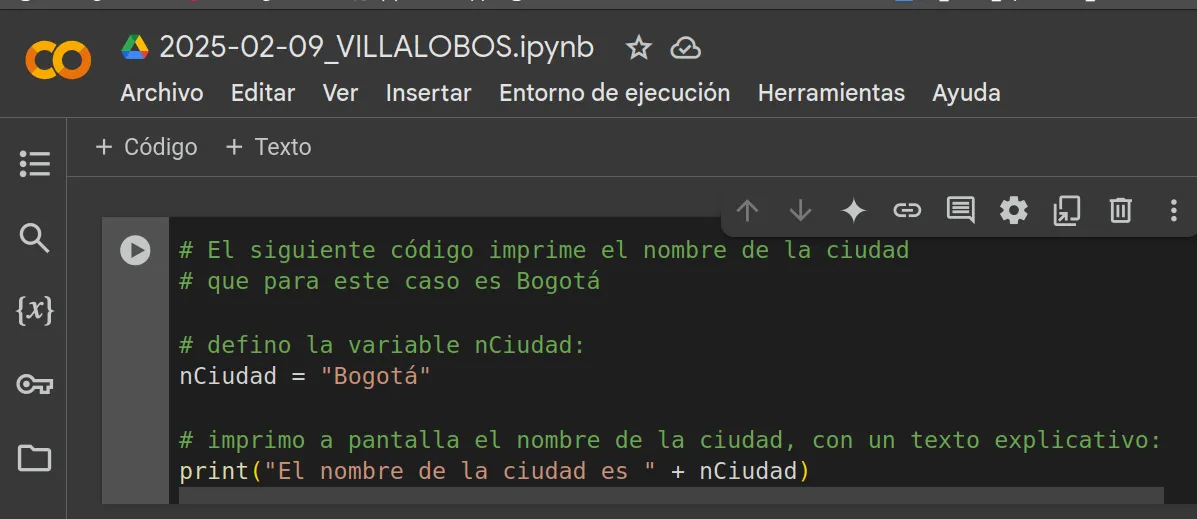
Primer Ejercicio en clase

El objetivo de este ejercicio es determinar cuál de los siguientes conjuntos de datos tiene un mayor promedio y cuál tiene mayor desviación estándar:

• Muestra 1: 9, 9, 10, 11, 12, 12

• Muestra 2: 4, 5, 6, 7, 8, 9

Primer punto

Antes de hacer los cálculos diga, ¿cuál de las dos muestras espera que tenga una mayor desviación estándar? ¿un mayor promedio? Responda esto en un comentario o en un bloque de texto.

Segundo punto

1. Defina la variable muestra1 como una lista, que tiene los valores que están atrás. Si no recuerda cómo se hace una lista, repase al final de Variables

2. Utilice la función sum para calcular el total de la muestra1, y asígnelo a la variable total1

   $total_1 = ...$

3. Calcule el promedio de muestra1, dividiendo total1 por el número de elementos de muestra1. Asígnelo a promedio1:

   $\overline{x}_1 = total_1 / ...$

4. La desviación estándar de la muestra se calcula como:

   $S = \sqrt{\frac{\sum_1^n (x_i - \overline{x})^2}{n-1}}$

   En este caso, sería:

   $S = \sqrt{\frac{(\overline{x}_1 - 9)^2 + (\overline{x}_1 - 9)^2 + (\overline{x}_1 - 10)^2 + (\overline{x}_1 - 11)^2 + (\overline{x}_1 - 12)^2 + (\overline{x}_1 - 12)^2}{n-1}}$

   Donde $n$ es el tamaño de la muestra y $\overline{x}_1$ el promedio que calculó atrás. Para calcular la desviación estándar podemos comenzar por calcular la varianza:

   $S_1^2 = \frac{(\overline{x}_1 - 9)^2 + (\overline{x}_1 - 9)^2 + (\overline{x}_1 - 10)^2 + (\overline{x}_1 - 11)^2 + (\overline{x}_1 - 12)^2 + (\overline{x}_1 - 12)^2}{n-1}$

   (en el software puede ser s1cuadrado = ... )

   Y luego la desviación estándar sacando la raíz:

   $S_1 = \sqrt{S_1^2}$

   (en el software sería s1 = sqcuadrado**0.5)

5. Ahora haga lo mismo para la muestra 2. Es decir, defina muestra2, total2, promedio2, etc.

6. Para confirmar, calcule ahora promedios usando np.mean

7. Para la desviación estándar se usa np.std. como se trata de una desviaciónn estándar muestral y no poblacional es necesario usar la variable ddof=1. Es decir, por ejemplo para la desviación estándar de la muestra 1 se usaría:

   np.std(muestra1,ddof=1)
   

Tercer punto

Los cálculos que hizo en el punto 2, ¿confirman lo que había dicho en el punto 1? Explique. Incluya la respuesta como un comentario.

Enviar

Envíe el archivo .ipynb por correo electrónico a mi correo electrónico, gabriel.villalobos@ esap …