Table of contents
Open Table of contents
Tipos de Distribuciones
Una distribución de valores de una variable es el conjunto de valores que tiene esa variable, ya sea sobre una población o sobre una muestra. Existen diferentes tipos de distribuciones.
Distribución de Frecuencia
Son tablas que representan el conteo (frecuencia) de los valores que tiene una variable agrupados en una serie de intervalos contiguos, no superpuestos. Se usan para establecer cómo están agrupadas las observaciones de una variable.
Ejemplo: Tardanzas de una empresa en 57 días
(Contento, página 71)
En una empresa se contabiliza el número de personas que llegan tarde a
una empresa cada día. Registramos los valores en un arreglo de
Python así:
tardanzas = [68, 63, 42, 27, 30, 36, 28, 32, 79, 27, 22, 23, 24, 25, 44, 65, 43, 25, 74, 51, 36, 42, 28, 31, 28, 25, 45, 12, 57, 51, 12, 32, 49, 38, 42, 27, 31, 50, 38, 21, 16, 24, 69, 47, 23, 22, 43, 27, 49, 28, 23, 19, 46, 30, 43, 49, 12]
En el curso de estadística descriptiva se vió la fórmula de Sturges, que recomienda el número de divisiones que debe tener un histograma
o equivalentemente
En este caso:
import numpy as np
h = 1 + 3.322 np.log10(57)
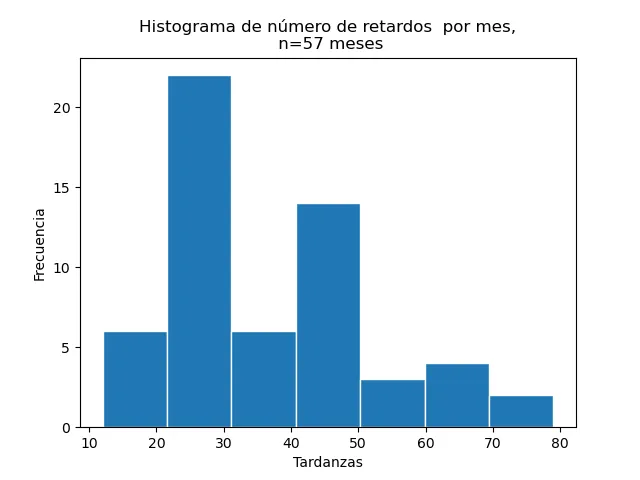
Obtenemos divisiones. Se puede hacer el histograma con matplotlib:
import matplotlib.pyplot as plt
plt.hist(tardanzas,bins=7,edgecolor='w')
plt.title("Histograma de número de retardos por mes,\n n=57 meses")
plt.xlabel("Tardanzas")
plt.ylabel("Frecuencia")
La primera línea carga la librería matplotlib. La segunda línea genera un histograma del objeto tardanzas que habíamos definido antes, usando blanco para el borde de las clases. La tercera línea asigna el título al histograma. Luego viene la etiqueta del eje x y la del eje y.
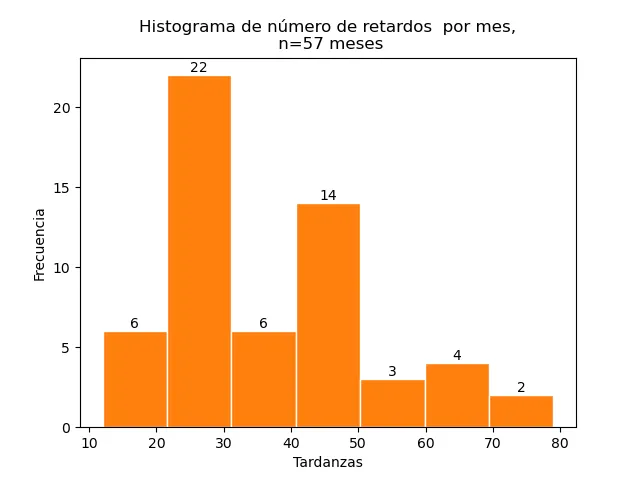
Si se quiere incluir la cuenta hay que modificar ligeramente el
código. Primero se incluye tres variables a la izquierda del comando
plt.hist, una para las cuentas, otra para los boredes y otra para
las barras. Luego se usa el comando plt.bar_label con argumento
barras.
cuentas,bordes,barras = plt.hist(tardanzas,bins=7, edgecolor='w')
plt.bar_label(barras)
plt.title("Histograma de número de retardos por mes, n=57 meses")
plt.xlabel("Tardanzas")
plt.ylabel("Frecuencia")
Ejercicio en clase
Usando los datos que se encuentran en el libro de Contento, pg. 87, ejercicio 7, “salinidad”, vamos a construir un histograma:
- Calcule el número de divisiones según Sturges,
- Ingrese los datos en una lista llamada salinidad ⌨️.
- Construya un histograma, con ese número de divisiones , sin el conteo. No copie y pegue ls instrucciones, tecléelas ⌨️.
- Modificque el algoritmo para incluir el conteo. No copie y pegue ls instrucciones, tecléelas ⌨️.
Distribuciones Discretas de Probabilidad
Variable discreta
Una variable es discreta cuando los valores que puede tomar la variable es un número contable. Ejemplos:
- Número de hijos nacidos vivos
- Máximo nivel educativo obtenido
Distribuciones de probabilidad
Las distribuciones de probabilidad son funciones que asignan a un valor de la probabilidad a un evento. Tienen dos características:
Si X es una variable discreta, la función de probabilidad para X es con . Se lee “la probabilidad de que X tenga el valor x”.
Debe cumplir dos condiciones:
- .
Por ejemplo, en un dado de 6 caras los eventos son los valores del 1 al 6. La probabilidad es
| x | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| f(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Se puede ver que cada valor de probabilidad es mayor o igual a cero y que la suma de las probabilidades es 1.
Ejercicio en clase: un dado de 10 caras

Escriba ¿cuál es la probabilidad de obtener el valor 7 al lanzar un dado que tuviese 10 caras?
Coeficientes de Asimetría y Curtosis
- El coeficiente de asimetría de una distribución es:
En Python se puede calcular usando la librería scipy.stats
import numpy as np
from scipy.stats import kurtosis, skew
Para la distribución de tardanzas:
skew(tardanzas)
- La curtosis de una distribución es:
En
Pythonse usa tambiénscipy.stats, como habíamos dicho, confrom scipy.stats import kurtosis. Para la districubión de tardanzas:
kurtosis(tardanzas)
Cuantiles
Los cuantiles dividen las observaciones en 4 grupos, cada uno con el
25% de las observaciones. En Python se pueden calcular usando la
función mquartiles de scipy.stats. Por ejemplo para las tardanzas
tenemos:
from scipy.stats import mquantiles
mquantiles(tardanzas)
Se obtienen los valores [25. , 32. , 46.3]. ¿cómo interpreta el valor ?
Probabilidad clásica (teórica) de una variable discreta
Hay algunos casos en los que se puede saber cuál es la posibilidad de una variable discreta. El mas sencillo es el caso en que todas las opciones tienen la misma probabilidad. Por ejemplo si en una oficina de atención al cliente hay 2 cabinas idénticas la probabilidad de que una persona elija al azar la cabina 1 o la cabina 2 es la misma. Esta es la probabilidad uniforme discreta.
Distribución uniforme discreta
Si es una variable aleatoria que puede tomar valores distintos , cada uno de ellos con el mismo chance de selección. La distribución de probabilidad para la variable aleatoria es:
La variable aleatoria uniforme discreta con valores enteros de 1 a se nota:
En el ejemplo de las dos cabinas de atención al cliente . Si es la probabilidad de que se elija izquierda o derecha: . Aquí etiquetamos y , luego:
Muestras de Distribuciones discretas en Python
Para construir una muestra de una lista en python se puede usar la
función random.choice de la librería numpy. Esta genera una
muestra aleatoria de un arreglo (lista) del tamaño definido por el
usuario.
Por ejemplo, arange(10) genera los números del 0 al 9. Veamos:
import numpy as np
lista10 = arange(10)
-
¿qué hacen estas instrucciones?
-
¿cómo vemos qué se ha definido en
lista10?
Para hallar 5 números elegidos al azar entre el 0 y el 10, se usa el siguiente código:
random.choice(lista10,5)
-
¿cómo se hace una muestra de tamaño 1000 de los números de 0 a 9?
-
Revise la ayuda de la función, e identifique ¿cómo se hace una lista que tenga los 10 números desde 0 hasta 9, sin repetir número?
-
¿cómo se hace una muestra, de tamaño 1000, de los números del 0 al 9, pero para la cual la probabilidad sea:
| x | p(x) |
|---|---|
| 0 | 0.04 |
| 1 | 0.08 |
| 2 | 0.12 |
| 3 | 0.16 |
| 4 | 0.2 |
| 5 | 0.16 |
| 6 | 0.12 |
| 7 | 0.08 |
| 8 | 0.04 |
| 9 | 0 |
Distribuciones Continuas
(en la siguiente sección )