Desarrollo axiomático de la probabilidad

Espacio Muestral

Conjunto de todos los posibles resultados de un experimento aleatorio. $\Omega$

Ejemplo

Lanzamiento de dos monedas: $\Omega = \{CC,CS, SC, SS\}$

Evento

Es un subconjunto del espacio muestral.

Ejemplo

Lanzar dos monedas y ambas salga Sello: SS

Eventos Excluyentes

Si $A$ y $B$ son dos eventos en $\Omega$, y $A \cap B = \emptyset$

Ley Aditiva de la probabilidad

Sean $A$ y $B$ dos eventos cualesquiera de $\Omega$. La probabilidad de la unión de $A$ y $B$ es: \ $P(A \cup B) = P(A) + P(B) - P(A\cap B)$

Ejemplo

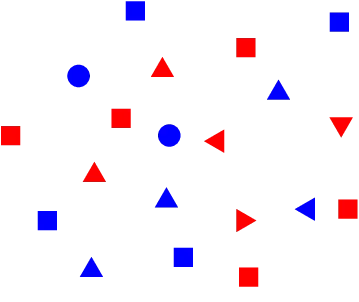
$A$: Figura roja.

$P(A)$ = $\frac{10}{20}$

$B$: Triángulo.

$P(B)$ = $\frac{9}{20}$

¿cuál es la probabilidad de que sea triángulo o que sea una figura roja?

$A \cup B$: sea triángulo o sea roja.

$P(A \cup B) = P(A) + P(B) - P(A\cap B)$

$P(A \cap B)$: sea triángulo rojo.

$P( A\cap B) = \frac{5}{20}$

$P(A \cup B) = \frac{10}{20} + \frac{9}{20} - \frac{5}{20} = \frac{14}{20}$

Probabilidad Conjunta, Marginal, y Condicional

Probabilidad Conjunta

Ocurren dos eventos

$P(FC) = P(F\cap C) = \frac{n_{FC}}{n}$

$P(FB) = P(F \cap B)= \frac{n_{FB}}{n}$ ,

Probabilidad Marginal

Es la probabilidad de un evento simple

$P(C) = \frac{n_{C}}{n}$ , y

$P(B) = \frac{n_{B}}{n}$

$P(F) = \frac{n_{F}}{n}$ , y

$P(N) = \frac{n_{N}}{n}$

Probabilidad Condicional

Ocurrencia de un evento, dado que se sabe que hay cierta característica. Probabilidad de que tenga color, dado que tiene fragancia. evento de interés, evento condicionante. $P(A/B)$ Las cond. por fila:

$P(C/F)= n_{CF}/n_F$

$P(B/F)=n_{FB}/n_F$

$P(C/N)= n_{CN}/n_N$

$P(B/N)=n_{BN}/n_N$

por col.:

$P(F/C)= n_{FC}/n_C$,

$P(N/C)=n_{NC}/n_C$

$P(F/B)= n_{FB}/n_B$,

$P(N/B)=n_{NB}/n_B$

Hay relación? $P(F/C)=\frac{n_{FC}}{n_c} ={n_{FC}}/{n_c} \cdot (\frac{1}{n}/\frac{1}{n}) = \frac{n_{FC}}{n} / \frac{n_c}{n} =$ $\frac{P(F\cap C)}{P(C)}$

Independencia Estadística

Dos eventos son independientes si la ocurrencia de uno no afecta la ocurrencia del otro. Numéricamente, los eventos $A$ y $B$ son independientes si:

$P(A/B) = P(A)$

Si se cumple esa condición, también:

$P(B/A) = P(B)$

$P(A \cap B) = P(A) \times P(B)$.

(y así sucesivamente, para A,B,C, $P(A \cap B \cap C) = P(A) \times P(B) \times P(C)$).

Ejemplo

A: ‘Mi médica es menor de 50 años’

B: ‘El Real Madrid le ajusta 8 goles a Millonarios’

Ejercicio

C y F son independientes?

$P(C/F) = \frac{n_{FC}}{n_C}$ $= \frac{12}{130} \approx 0.0923$

$P(C) = \frac{n_C}{n}$ $=62/200=0.31$

Teorema de Bayes (tema opcional)

Si $\Omega$, esp. mstr. con un exp. aleatorio, A evento cualq. en $\Omega$. Partición $\{B_i\}$

excluyentes: $\Omega = B_1 \cup B_2 \cup ... \cup B_k$,

independientes: $B_i \cap B_j = \emptyset$ ,

no nulos: $P(B_i) > 0$, las probabilidades condicionales $P(B_j / A)$, con $j=1,2,...,k$, son:

$P(B_j/A) = \frac{P(B_j)P(A/B_j)}{\sum_{i=1}^{k}P(B_i)P(A/B_i}$

Ejemplo

Un examen elección múltiple con única respuesta tiene 4 opciones. La probabilidad de que la estudiante sepa la respuesta es 0.8. ¿Cuál es la probabilidad de que, dada una p. al azar, conteste correctamente? Dado que respondió corrrectamente, ¿con qué P sabe la respuesta correcta?

Partición:$B_1$:sabe $B_2$:No sabe. Evento A: contestó correctamente.

$P(B_1)=0.8$,

$P(B_2)= 0.2$.

$P(A/B_1)= 1$,

$P(A/B_2)= 0.25$

$P(A)= P(A/B_1)P(B_1)+P(A/B_2)P(B_2)= 1\times 0.8+0.25\times 0.2=0.85$

$P(B_1/A)= \frac{P(A/B_1)P(B_1)}{P(A)}= \frac{0.8 \times 1}{0.85}\approx 0.9412$

Ley Multiplicativa de la Probabilidad

Dado que la probabilidad condicional de que ocurra el evento A dado el evento condicionante B es:

$P(A/B) = \frac{P(A \cap B)}{P(B)}$

Entonces podemos despejar la probabilidad de la intersección:

$P(A \cap B) = P(A/B) P(B)$

Ahora la \emph{probabilidad condicional} de que ocurra el evento B dado el evento condicionante A es:

$P(B/A) = \frac{P(A \cap B)}{P(A)}$

Entonces podemos despejar la probabilidad de la intersección:

$P(A \cap B) = P(B/A) P(A)$

La probabilidad de la intersección de dos eventos $P(A \cap B)$ se puede hallr con las probabilidades condicionales así:

$P(A \cap B) = P(A/B) P(B)$

$P(A \cap B) = P(B/A) P(A)$