Distribuciones continuas de probabilidad

Tienen las siguientes características:

• $f(x) \geq 0$
  La función de probabilidad es positiva.
• $\int_{-\infty}^{\infty} f(x) dx = 1$
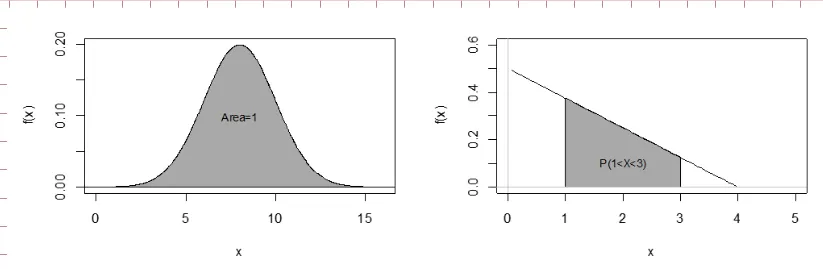
  El área bajo la curva de la densidad de probabilidad es 1.
• $P(a \leq X \leq b) = \int_a^b f(x) dx$
  La probabilidad de un evento entre $a$ y $b$ es la integral entre esos dos valores.

La segunda característica, integral igual a 1, se ve en la figura abajo izquierda. La segunda, probabilidad igual a área bajo la curva, en la figura de la derecha.

Ejemplo: Distribución uniforme continua

(Contento, pg. 196)

Dada una variable $X$, que puede tomar valores en el intervalo $[a,b]$, entonces la densidad uniforme contínua es:

$f(x) = \frac{1}{b-a}\ \ ; \ \ a \leq x \leq b$

La notación $X \sim U_c(a,b)$ se lee: x se distribuye uniforme contínua en el in tervalo a,b

Valor esperado y varianza de la distribución uniforme continua

$\mu = \frac{b+a}{2}$

$\sigma^2 = \frac{(b-a)^2}{12}$

Ejemplo (Contento, pg. 188)

La concentración de cierto contaminante está distribuida de manera uniforme en el intervalo $0$ a $20$ ppm. Si se considera tóxica una concentración de $8$ o más, responda las preguntas:

• ¿Con qué probabilidad al tomarse una muestra se encuentra una concentración tóxica? ¹.
• ¿Cuál es la concentración media? ¿la varianza?².
• ¿Con qué probabilidad la concentración es exactamente 10?

Distribución normal

Una buena explicación de la distribución normal está en éste video del profesor Leandro González: https://youtu.be/-fD8KmtsI1M

Un grán número de variables del mundo real resultan tener una distribución normal. Por ejemplo:

• Características morfológicas: como talla, peso, long. total o parcial
• Características fisiológicas: como el efecto de dosis de un fármaco, o de cantidad de abono
• Características sociológicas: como el consumo de productos por grupos humanos
• Características psicológicas: como el CI, o grado de adaptación a un medio
• Características físicas: como la resistencia a rotura de piezas, vida útil de un producto, tiempo de traslado.

Relación normal - binomial (Máquina de Galton)

• https://youtu.be/1DTRzPRfu6s
• https://youtu.be/47nP4IkD62k

Características de la distribución normal

• $X \in \mathcal{R}$
• $f$ simétrica
• mediana = moda
• Asintótica al eje x.
• $\int_{-\infty}^{\infty} f dx = 1$
• $\int_{\mu-\sigma}^{\mu + \sigma} f dx \approx 0.6827$
• $\int_{\mu-2\sigma}^{\mu + 2\sigma} f dx \approx 0.9545$
• $\int_{\mu-3\sigma}^{\mu + 3\sigma} f dx \approx 0.9973$
• $f(x) = \frac{1}{\sqrt{2 \pi \sigma}}e^{-\frac{1}{2} \left( \frac{x - \mu}{\sigma}\right)^2},$ $x$ es un número real, $\mu$ también, $\sigma$ es un número positivo.

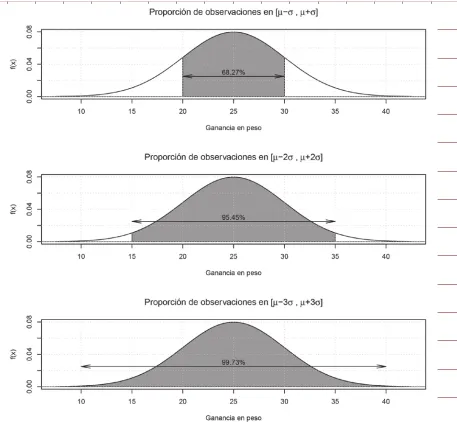
Distribución normal estándar

Es una distribución normal para la que $\mu=0$ y $\sigma=1$

$f(z) = \frac{1}{\sqrt{2 \pi }}e^{-\frac{1}{2} z^2}$

Recursos:

• Calculadora en línea DESMOS: https://www.desmos.com/calculator

• Página de Matt Bognar https://homepage.divms.uiowa.edu/~mbognar/

• Applet Distribución Normal Matt Bognar https://homepage.divms.uiowa.edu/~mbognar/applets/normal.html

Evaluación

En Khan Academy

Hacer los ejercicios:

• Distribución Normal, área entre dos puntos

• Distribución Normal, área por encima o por debajo de un punto

Notas a pie